Unterabschnitte
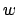 in der Sprache des DFAs enthalten ist. Wir simulieren hierfür den DFA. Das Wortproblem kann in linearer Zeit entschieden werden, nämlich in
in der Sprache des DFAs enthalten ist. Wir simulieren hierfür den DFA. Das Wortproblem kann in linearer Zeit entschieden werden, nämlich in 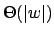 . Für NFAs kann das Wortproblem in exponentieller Zeit gelöst werden, da vorerst der Automat in einen Potenzautomaten umgeformt werden muß, da ein Potenzautomat immer
. Für NFAs kann das Wortproblem in exponentieller Zeit gelöst werden, da vorerst der Automat in einen Potenzautomaten umgeformt werden muß, da ein Potenzautomat immer 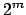 Zustände hat, wobei m die Anzahl der Zustände des Orignial-DFAs.
Zustände hat, wobei m die Anzahl der Zustände des Orignial-DFAs.
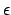 enthält und somit nicht leer ist.
enthält und somit nicht leer ist.
Die Laufzeit hierfür ist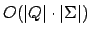 .
.
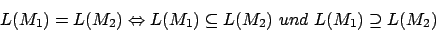
Für den Inklusionstest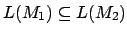 können wir folgendes ausnutzen:
können wir folgendes ausnutzen:
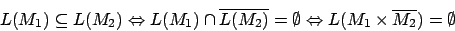
Wir bilden also zwei Mal den Produktautomaten aus
Die Laufzeit für dieses Verfahren ist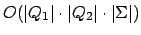
Algorithmen zur Feststellung von Eigenschaften
Das Wortproblem
Das Wortproblem ist die Frage ob ein WortLeerheitstest
Man prüfe, ob der Automat Endzustände hat, die erreichbar sind. Hat er davon keine, so ist die Sprache leer. Andernfalls ist sie es nicht. Beachte, daß wenn der Startzustand Endzustand ist, die Sprache das WortDie Laufzeit hierfür ist
Äquivalenztest
Es giltFür den Inklusionstest
Wir bilden also zwei Mal den Produktautomaten aus
- einmal der einen Sprache normal und der anderen Sprache negiert und
- einmal aus der einen Sprache negiert und aus der anderen normal
Die Laufzeit für dieses Verfahren ist
Endlichkeitstest
Um zu testen, ob eine Sprache endlich ist, wenden wir auf dem Automaten ähnliche Algorithmen, wie schon aus der Algorithmik bekannt an.- Zuerst entfernen wir alle Zustände und die dazugehörigen Kanten, die nicht vom Startzustand aus erreicht werden können.
- Dann bilden wir den inversen Graphen
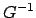 .
.
- Wir prüfen, ob von einem Endzustand dieses Graphens irgendein Zyklus erreicht werden kann. Die Zyklen sind genau dieselben, wie in dem Graphen
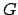 . Wir können Zyklen mit Hilfe der DFS-Kantenklassifizierung finden. Ein Zyklus exisitert dann, wenn es Rückwärtskanten gibt.
. Wir können Zyklen mit Hilfe der DFS-Kantenklassifizierung finden. Ein Zyklus exisitert dann, wenn es Rückwärtskanten gibt.