Unterabschnitte
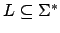 eine reguläre Sprache. Dann gibt es eine ganze Zahl
eine reguläre Sprache. Dann gibt es eine ganze Zahl 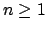 , so daß jedes Wort
, so daß jedes Wort 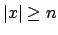 wie folgt zerlegt werden kann:
wie folgt zerlegt werden kann:
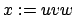 mit Wörtern
mit Wörtern
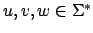 , so daß
, so daß
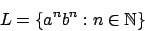
mit einem DFA zu entscheiden, da er nicht festhalten kann, wie groß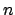 ist.
ist.
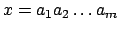 mit
mit 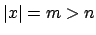 ein Wort in
ein Wort in 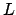 , wobei
, wobei 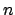 die Anzahl der Zustände des DFAs.
die Anzahl der Zustände des DFAs.
Dann ist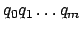 der Lauf im DFA, wobei
der Lauf im DFA, wobei 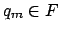 .
.
Da die Anzahl der Zustände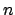 ist und der Lauf größer ist, müssen Zustände mehrfach besucht werden. D.h. wir gehen eine Schleife im Graphen für das Teilwort
ist und der Lauf größer ist, müssen Zustände mehrfach besucht werden. D.h. wir gehen eine Schleife im Graphen für das Teilwort 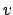 .
.
Es gibt Indizes, so daß gilt (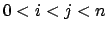 )
)
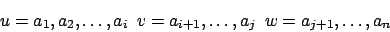
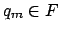 ist jedes dieser Worte in der Sprache enthalten.
ist jedes dieser Worte in der Sprache enthalten.
Pumping Lemma für reguläre Sprachen
Definition
Sei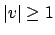
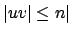
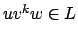 für alle
für alle
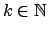
Kernaussage
Die Kernaussage des Pumping Lemmas ist es, daß Autmaten keinen unbeschränkten Speicher haben, mit welchem sie zählen könnten. Es ist nicht möglich Sprachen von Typ (oder ähnlichen Typs)mit einem DFA zu entscheiden, da er nicht festhalten kann, wie groß
Beweis
SeiDann ist
Da die Anzahl der Zustände
Es gibt Indizes, so daß gilt (
- Wegen
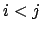 gilt
gilt 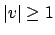
- Wegen
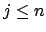 gilt
gilt
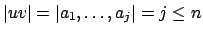
- Wir können das Wort in
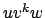 unterteilen, da der Zustand zu dem Zeichen
unterteilen, da der Zustand zu dem Zeichen 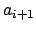 gehörig, mehrfach besucht wird und wir beliebig häufig diesen besuchen können.
gehörig, mehrfach besucht wird und wir beliebig häufig diesen besuchen können.
Beispiele
-
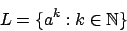
Diese Sprache ist regulär, da wir
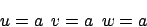
wählen können und Regel 1 erfüllt ist, daß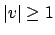 , Regel 2 erfüllt ist, da
, Regel 2 erfüllt ist, da 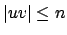 (jedes Wort hat mindestens 3 Zeichen) und Regel 3 auch erfüllt ist, da wir das
(jedes Wort hat mindestens 3 Zeichen) und Regel 3 auch erfüllt ist, da wir das 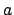 beliebig wiederholen dürfen und das zusammengesetzte Wort immer noch in der Sprache ist.
beliebig wiederholen dürfen und das zusammengesetzte Wort immer noch in der Sprache ist.
-
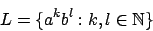
Diese Sprache ist regulär, da wir
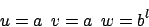
wählen können und alle Regeln wiederum nicht verletzt sind, ganz besonders die Regel 3 nicht verletzt ist. -
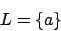
Diese Sprache ist auch regulär, jedoch ist das einzige Wort welches gebildet werden kann nur 1 Zeichen lang, weshalb diese Sprache nicht mit dem Pumping Lemma überprüft werden kann, ob sie denn wirklich regulär ist. -
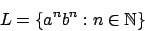
Diese Sprache ist nicht regulär, da wir sie nicht richtig unterteilen können.
Sei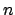 die Zahl aus dem Pumping Lemma. Da
die Zahl aus dem Pumping Lemma. Da 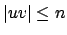 kann
kann 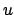 nur aus
nur aus 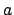 s bestehen. Dann muß
s bestehen. Dann muß 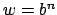 sein. Da aber auch
sein. Da aber auch 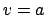 , können auch Wörter
, können auch Wörter
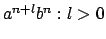 gebildet werden. Dies ist ein Widerspruch zu den Eigenschaften der oben definierten Sprache
gebildet werden. Dies ist ein Widerspruch zu den Eigenschaften der oben definierten Sprache 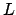 .
.