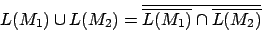Unterabschnitte
NFAs mit
Wir können in NFAs 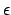 -Übergänge51 definieren. Bei
-Übergänge51 definieren. Bei 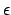 -Übergängen verbraucht der NFA keine Eingabe. Er kann
-Übergängen verbraucht der NFA keine Eingabe. Er kann 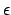 -Übergänge spontan nichtdeterminitisch ausführen (dann wenn es so erforderlich ist, damit das Eingabewort möglichst akzeptiert).
-Übergänge spontan nichtdeterminitisch ausführen (dann wenn es so erforderlich ist, damit das Eingabewort möglichst akzeptiert).
Das jeder NFA in einen NFA mit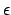 -Übergängen überführt werden kann, ist klar. Wir brauchen nichts zu machen.
-Übergängen überführt werden kann, ist klar. Wir brauchen nichts zu machen.
Jeder NFA mit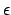 -Übergängen kann auch in einen NFA ohne
-Übergängen kann auch in einen NFA ohne 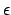 -Übergänge umgeformt werden. Dazu ,,überbrücken'' wir sozusagen die
-Übergänge umgeformt werden. Dazu ,,überbrücken'' wir sozusagen die 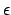 -Übergänge:
-Übergänge:
Sei
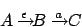
der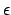 -Übergang, noch gefolgt von einem anderen Übergang.
-Übergang, noch gefolgt von einem anderen Übergang.
Vereinigung -
Wir fassen beide NFAs als einen auf. Es wird nichtdeterministisch entschieden, welcher Startzustand verwendet wird. Entweder der von Automat 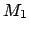 oder
oder 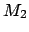 .52
.52
Durchschnitt -
Komplement -
Wir gehen von einem Automaten hierbei aus, der eine totale Übergangsfunktion hat, d.h. das wir alle Übergänge, die nicht mehr ,,weitergehen'' in einen Fangzustand leiten.
Wir erhalten die Komplementsprache, indem wir alle Endzustände zu normalen Zuständen machen und alle normalen Zustände zu Endzuständen.
Konkatenation -
Wir können zwei NFAs hintereinanderschalten, indem wir aus dem Endzustand von 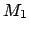 einen normalen Zustand machen und von diesem mit einem
einen normalen Zustand machen und von diesem mit einem 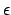 -Übergang in
-Übergang in 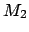 überleiten.
überleiten.
Kleenabschluß -
Verknüpfungen regulärer Sprachen
NFAs mit 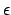 -Übergängen
-Übergängen
Wir können in NFAs Das jeder NFA in einen NFA mit
Jeder NFA mit
Sei
der
- Wir entfernen die Regel
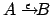
- Wir fügen
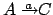 hinzu.
hinzu.
- Falls es eine Übergangsfunktion
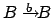 gegeben hat, dann fügen wir
gegeben hat, dann fügen wir
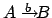 und lassen
und lassen
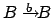 . Des weiteren lassen wir auch
. Des weiteren lassen wir auch
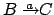 stehen.
stehen.
Vereinigung -
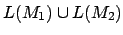
Wir fassen beide NFAs als einen auf. Es wird nichtdeterministisch entschieden, welcher Startzustand verwendet wird. Entweder der von Automat
Durchschnitt -
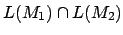
- Wir bilden einen Produktautomaten, indem wir einen jeden Knoten des Automatens
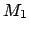 mit allen Knoten des Automatens
mit allen Knoten des Automatens 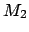 multiplizieren. In einem Zustand des Produktautomaten stehen dann also zwei Zustände.
multiplizieren. In einem Zustand des Produktautomaten stehen dann also zwei Zustände.
- Wir zeichnen eine Übergangsfunktion zwischen den beiden Zuständen mit der Inschrift
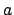 , wenn es zwischen den einzelnen Zuständen in den Produktzuständen auch zwei Übergangsfunktionen mit Inschrift
, wenn es zwischen den einzelnen Zuständen in den Produktzuständen auch zwei Übergangsfunktionen mit Inschrift 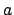 gegeben hat. Also:
gegeben hat. Also:
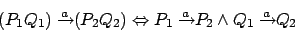
Komplement -
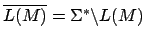
Wir gehen von einem Automaten hierbei aus, der eine totale Übergangsfunktion hat, d.h. das wir alle Übergänge, die nicht mehr ,,weitergehen'' in einen Fangzustand leiten.
Wir erhalten die Komplementsprache, indem wir alle Endzustände zu normalen Zuständen machen und alle normalen Zustände zu Endzuständen.
Konkatenation -
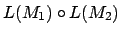
Wir können zwei NFAs hintereinanderschalten, indem wir aus dem Endzustand von
Kleenabschluß -
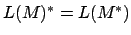
- Wir gehen vom Endzustand wieder in den Startzustand mit einem
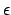 -Übergang. Hiermit akzeptieren wir beliebig oft Wörter, die mit
-Übergang. Hiermit akzeptieren wir beliebig oft Wörter, die mit 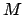 gebildet worden sind.
gebildet worden sind.
- Desweiteren fügen wir zusätzlich noch einen Endzustand hinzu, der im NFA auch gleichzeitig Startzustand wird. Hiermit akzeptieren wir das leere Wort.
Fußnoten
- ...-Übergänge51
- Diese heißen z.B. auch
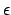 -Moves
-Moves
- ....52
- Vereinigen wir zwei DFAs, so können wir auch die Morgansche Regel anwenden, um die Potenzmengenkonstruktion, die wir anwenden müssen, um aus dem entstehenden NFA wieder einen DFA zu machen, zu umgehen: