Unterabschnitte
Bei der Guess and Check-Methode wird eine Kombination mit Hilfe des ,,Orakels'' einfach geraten. Dabei wird so geraten, daß direkt das richtige Ergebnis geraten wird. Gibt es kein richtiges Ergebnis, so wird ein falsches Ergebnis ausgegeben. Das von dem nichtdeterministischen Guess-Bereich erratene Ergebnis wird im deterministischen Check-Bereich noch einmal auf Richtigkeit überprüft. Hier stellt sich heraus, ob es wirklich richtig ist oder ob die Guess-Methode ein falsches Ergebnis zurückgegeben hat, weil es kein richtiges gibt.
SAT
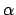 : Die zu überprüfende Formel, wobei z.B.
: Die zu überprüfende Formel, wobei z.B.
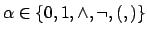
Wir raten zunächst mit Hilfe des ,,Orakels'' eine Belegung der Formel. Ist das SAT-Problem erfüllbar, bekommen wir eine erfüllbare Belegung zurück. Wenn nicht irgendeine Belegung.
Dann können wir in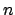 Schritten überprüfen, ob die geratene Belegung tatsächlich eine wahre Belegung ist.
Schritten überprüfen, ob die geratene Belegung tatsächlich eine wahre Belegung ist.
Wir benötigen polynomielle Laufzeit für beide Teilalgorithmen, da die Anzahl der Literale durch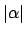 beschränkt ist.
beschränkt ist.
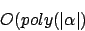
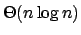 , unter dem nichtdeterministischen Kostenmaß die Laufzeit
, unter dem nichtdeterministischen Kostenmaß die Laufzeit 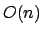 .
.
Dies kommt dadurch zustande, daß wir mit Guess-Methode einen möglichen Teiler raten. Es wird ein Teiler der zu testenden Zahl geraten, wenn es einen gibt. Andernfalls wird irgendeine Zahl geraten. Nachdem wir den möglichen Teiler geraten haben, können wir testen, ob dieser geratene Teile wirklich Teiler der zu testenden Zahl ist.
Man kann den Graph G folgendermaßen codieren:
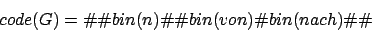
Kodierung des CP
Man kann das gesamte CP folgendermaßen kodieren:
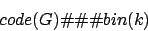
Eingabegröße des CP
Die Eingabegröße ist also
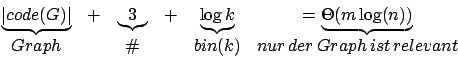
Laufzeit des CP
Für ein deterministisches Verfahren können wir für die untere Schranke die Laufzeit mit
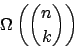
festlegen. Dies beruht auf der Tatsache, daß wir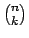 Möglichkeiten haben, eine k-er Clique aus allen Knoten auszuwählen23. Wir testen jede Clique in konstanter Zeit.
Möglichkeiten haben, eine k-er Clique aus allen Knoten auszuwählen23. Wir testen jede Clique in konstanter Zeit.
Es gilt die Abschätzung:
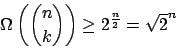
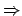 exponentielle Laufzeit24
exponentielle Laufzeit24
NP
NP liegt in EXPTIME
Dies können wir beweisen, indem wir die NTM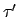 , die den NP-Algorithmus ausführt mit einer deterministischen DTM
, die den NP-Algorithmus ausführt mit einer deterministischen DTM  in EXPTIME simulieren.
in EXPTIME simulieren.
Es liegt ein Berechnungsbaum vor, welchen wir mit Hilfe einer Breitensuche oder einem Preorderdurchlauf durchgehen. Da die nichtdeterministische Turingmaschine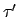 polynomiell beschränkt ist, ist die maximale Tiefe des Baumes polynomiell beschränkt.
polynomiell beschränkt ist, ist die maximale Tiefe des Baumes polynomiell beschränkt.
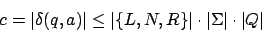
somit gilt für die Knotenanzahl
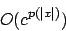
Also ist die Simulation von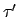 exponentiell beschränkt
exponentiell beschränkt
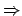 NP
NP 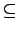 EXPTIME
EXPTIME
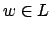 von der Turingmaschine
von der Turingmaschine  in
in 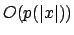 akzeptiert werden, können wir die gesamte Turingmaschine beschränken, indem wir alle irgendwann verwerfenden oder endlosen Berechnungen abschneiden, wenn sie über polynomielle Laufzeit hinaus laufen.
akzeptiert werden, können wir die gesamte Turingmaschine beschränken, indem wir alle irgendwann verwerfenden oder endlosen Berechnungen abschneiden, wenn sie über polynomielle Laufzeit hinaus laufen.
- SAT - Guess and Check Methode
- Primzahlen
- Cliquenproblem
- Zeitkomplexitätsklassen
- P,NP,EXPTIME
- NP
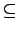 EXPTIME
EXPTIME
- Polynomialzeit akzeptierende NTMs
Zeitkomplexität
SAT - Guess and Check Methode
Guess and Check-MethodeBei der Guess and Check-Methode wird eine Kombination mit Hilfe des ,,Orakels'' einfach geraten. Dabei wird so geraten, daß direkt das richtige Ergebnis geraten wird. Gibt es kein richtiges Ergebnis, so wird ein falsches Ergebnis ausgegeben. Das von dem nichtdeterministischen Guess-Bereich erratene Ergebnis wird im deterministischen Check-Bereich noch einmal auf Richtigkeit überprüft. Hier stellt sich heraus, ob es wirklich richtig ist oder ob die Guess-Methode ein falsches Ergebnis zurückgegeben hat, weil es kein richtiges gibt.
SAT
Wir raten zunächst mit Hilfe des ,,Orakels'' eine Belegung der Formel. Ist das SAT-Problem erfüllbar, bekommen wir eine erfüllbare Belegung zurück. Wenn nicht irgendeine Belegung.
Dann können wir in
Wir benötigen polynomielle Laufzeit für beide Teilalgorithmen, da die Anzahl der Literale durch
Primzahlen
Unter dem deterministischen. logarithmischen Kostenmaß hat der Primzahltest die LaufzeitDies kommt dadurch zustande, daß wir mit Guess-Methode einen möglichen Teiler raten. Es wird ein Teiler der zu testenden Zahl geraten, wenn es einen gibt. Andernfalls wird irgendeine Zahl geraten. Nachdem wir den möglichen Teiler geraten haben, können wir testen, ob dieser geratene Teile wirklich Teiler der zu testenden Zahl ist.
Cliquenproblem
Kodierung des GraphenMan kann den Graph G folgendermaßen codieren:
Kodierung des CP
Man kann das gesamte CP folgendermaßen kodieren:
Eingabegröße des CP
Die Eingabegröße ist also
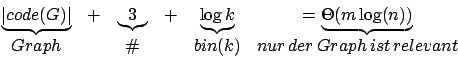
Laufzeit des CP
Für ein deterministisches Verfahren können wir für die untere Schranke die Laufzeit mit
festlegen. Dies beruht auf der Tatsache, daß wir
Es gilt die Abschätzung:
Zeitkomplexitätsklassen
Es gibt folgende Klassen im deterministischen und im nichtdeterministischen:| DTIME | NTIME |
| DSPACE | NSPACE |
P,NP,EXPTIME
|
|
|
|
|
|
NP 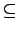 EXPTIME
EXPTIME
NP liegt in EXPTIME
Dies können wir beweisen, indem wir die NTM
Es liegt ein Berechnungsbaum vor, welchen wir mit Hilfe einer Breitensuche oder einem Preorderdurchlauf durchgehen. Da die nichtdeterministische Turingmaschine
Der Verzweigungsgrad ![]() jedes Knotens dieses Baumes ist
jedes Knotens dieses Baumes ist
somit gilt für die Knotenanzahl
Also ist die Simulation von
Polynomialzeit akzeptierende NTMs
Auf wenn nur WörterFußnoten
- ... auszuwählen23
- Kombinatorik
- ... Laufzeit24
- Das Nichtdeterministische Verfahren für das CP hat polynomielle Laufzeit.