Unterabschnitte
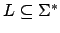 ist genau dann
ist genau dann 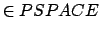 , wenn gilt:
, wenn gilt:
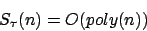
SAT
Man kann mit Hilfe eines Backtrackingalgorithmus25 die NTM für SAT simulieren. Die Simulation belegt nur polynomiellen Platz, nämlich soviel Platz wie die Länge der Formel26: 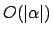 . (Dieser Beweis ist ähnlich dem von
. (Dieser Beweis ist ähnlich dem von
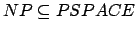 )
)
In-Place Acceptance
In-Place-Acceptance bedeutet, daß die Turingmaschine 
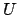 , die mitzählt, wieviel Bandzellen
, die mitzählt, wieviel Bandzellen  benutzt:
benutzt:
NP
Wir benutzen eine Tiefensuche, um den Berechnungsbaum von der Turingmaschine, welche in NP liegt zu durchgehen.
Die Rekursionstiefe ist durch ein Polynom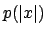 beschränkt (Definition von
beschränkt (Definition von 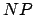 ). Bei einem PTIME-Algorithmus darf der Berechnungsbaum höchstens polynomielle Tiefe haben, um die Rekursion zu speichern. Das ist hier erfüllt.
). Bei einem PTIME-Algorithmus darf der Berechnungsbaum höchstens polynomielle Tiefe haben, um die Rekursion zu speichern. Das ist hier erfüllt.
PSPACE
Die Turingmaschine in 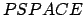 ist im Platz durch ein Polynom
ist im Platz durch ein Polynom 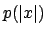 beschränkt. Er ergibt sich für die Gesamtanzahl der Konfigurationen27 der Turingmaschine:
beschränkt. Er ergibt sich für die Gesamtanzahl der Konfigurationen27 der Turingmaschine:
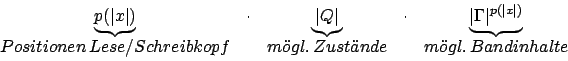
Wir können eine Konstante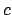 finden, so dass gilt:
finden, so dass gilt:
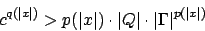
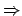 exponentiell beschränkt
exponentiell beschränkt
Satz von Savitch:
Haben wir keinen Beweis (glücklicherweise) gemacht
Wir haben nur gesagt, daß nach diesem Satz gilt:
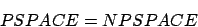
- PSPACE
- SAT
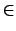 PSPACE
PSPACE
- In-Place Acceptance
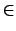 PSPACE
PSPACE
- NP
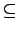 PSPACE
PSPACE
- PSPACE
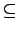 EXPTIME
EXPTIME
- Satz von Savitch:
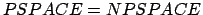
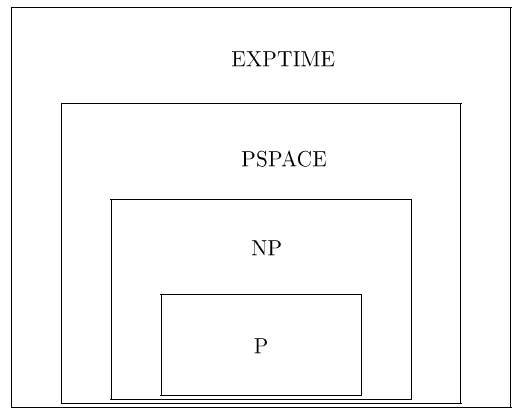
- Übersicht über die Komplexitätsklassen
Platzkomplexität
PSPACE
Eine Sprache
SAT 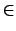 PSPACE
PSPACE
Man kann mit Hilfe eines Backtrackingalgorithmus25 die NTM für SAT simulieren. Die Simulation belegt nur polynomiellen Platz, nämlich soviel Platz wie die Länge der Formel26:
In-Place Acceptance 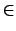 PSPACE
PSPACE
In-Place-Acceptance bedeutet, daß die Turingmaschine - in
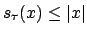 Platz
Platz
- akzeptiert oder verwirft.
- Wenn die Turingmaschine
 akzeptiert, akzeptiert die Turingmaschine
akzeptiert, akzeptiert die Turingmaschine 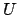 auch.
auch.
- Kommt sie über die erlaubte Anzahl
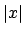 , der Länge des Eingabewortes, so verwirft sie.
, der Länge des Eingabewortes, so verwirft sie.
- Kommt eine Konfiguration doppelt vor (daran kann man erkennen, daß sie Turingmaschine endlos laufen wird), so verwirft sie.
Es liegt nun nahe, daß wir die alten Konfigurationen in der Turingmaschine einfach speichern. Dies würde allerdings zuviel Platz kosten. Statt dessen speichern wir die aktuelle Konfiguration und simulieren die gesamte Turingmaschiene noch einmal von Anfang an, generieren dabei alle alten Konfigurationen und vergleichen.
noch einmal von Anfang an, generieren dabei alle alten Konfigurationen und vergleichen.
NP 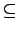 PSPACE
PSPACE
Wir benutzen eine Tiefensuche, um den Berechnungsbaum von der Turingmaschine, welche in NP liegt zu durchgehen.
Die Rekursionstiefe ist durch ein Polynom
PSPACE 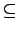 EXPTIME
EXPTIME
Die Turingmaschine in 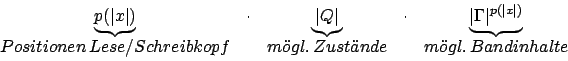
Wir können eine Konstante
Satz von Savitch:
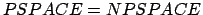
Haben wir keinen Beweis (glücklicherweise) gemacht
Wir haben nur gesagt, daß nach diesem Satz gilt:
Übersicht über die Komplexitätsklassen

Fußnoten
- ... Backtrackingalgorithmus25
- Tiefensuche
- ... Formel26
- sorry, doch keine Fussnote.
- ... Konfigurationen27
- Also Möglichkeiten, wie die Zeichen auf dem Band stehen können, Möglichkeiten wie der Zeiger stehen kann und Möglichkeiten in welchem Zustand sich die Turingmaschine momentan befindet.