Unterabschnitte
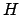 des Halteproblems ist
des Halteproblems ist
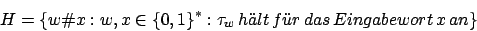
Die Sprache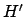 für das spezielle Halteproblem ist
für das spezielle Halteproblem ist
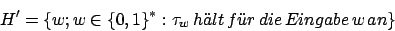
 konstruieren, die die Turingmaschine
konstruieren, die die Turingmaschine 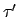 simuliert. Der Algorithmus, den
simuliert. Der Algorithmus, den 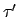 ausführt, soll überprüft werden, ob er bei der enthaltenen Eingabe terminiert. Die Turingmaschine
ausführt, soll überprüft werden, ob er bei der enthaltenen Eingabe terminiert. Die Turingmaschine  akzeptiert, sobald der
akzeptiert, sobald der 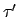 die Berechnung beendet hat. Wenn aber
die Berechnung beendet hat. Wenn aber 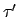 endlos läuft, dann akzeptiert auch
endlos läuft, dann akzeptiert auch  nie.
nie.  Semientscheidbarkeit
Semientscheidbarkeit
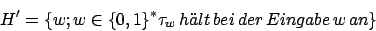
Definitionen: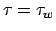 . D.h. der Halteproblemalgorithmus wird auf sich selbst angewendet.
. D.h. der Halteproblemalgorithmus wird auf sich selbst angewendet.
1.Fall:
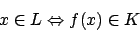
d.h. daß es eine totale Übergangsfunktion gibt, die aus jeder Eingabe für L eine Eingabe für K macht und daß L und K für die gleiche (für K vorher transformierte) Eingabe akzeptieren, verwerfen oder endlos laufen.
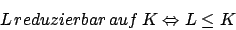
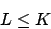
K entscheidbar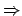 L entscheidbar
L entscheidbar
K semientscheidbar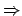 L semientscheidbar
L semientscheidbar
K unentscheidbar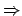 L unentscheidbar
L unentscheidbar
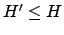 . Offenbar kann man das spezielle Halteproblem mit der Funktion
. Offenbar kann man das spezielle Halteproblem mit der Funktion
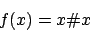
in das allgemeine Halteproblem überführen (da die DTM ja auf sich selbst angewendet wird). Somit ist dann genauso wie das spezielle Halteproblem auch das allgemeine Halteproblem unentscheidbar, da das spezielle Halteproblem ein Spezialfall des allgemeinen Halteproblem ist16 . Wir erhalten: Die Sprache H
ja auf sich selbst angewendet wird). Somit ist dann genauso wie das spezielle Halteproblem auch das allgemeine Halteproblem unentscheidbar, da das spezielle Halteproblem ein Spezialfall des allgemeinen Halteproblem ist16 . Wir erhalten: Die Sprache H
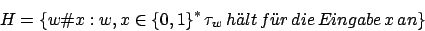
ist unentscheidbar.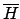 (das Komplement des Halteproblems)
(das Komplement des Halteproblems)
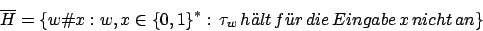
ist nicht semientscheidbar.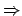 nicht semientscheidbar
nicht semientscheidbar
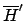 ist semientscheidbar. Wir definieren eine DTM
ist semientscheidbar. Wir definieren eine DTM  , so daß gilt:
, so daß gilt:
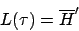
Unsere DTM akzeptiert oder läuft nur endlos. Verwerfen tut sie nicht.
akzeptiert oder läuft nur endlos. Verwerfen tut sie nicht.
Sei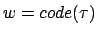 .
.
Wir setzen weiterhin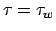 :
Es gilt:
:
Es gilt:
Widerspruch
- Die Sprache des Halteproblems und des speziellen Halteproblems
- Satz: Das Halteproblem ist unentscheidbar
- Informeller Beweis des Halteproblems mittels Halteproblemtabelle
- Das Halteproblem ist Semientscheidbar
- Spezielles Halteproblem
- Reduktion
- Reduktionsprinzip
- Unentscheidbarkeit des Halteproblems
- Die Nicht-Semientscheidbarkeit des Komplements des Halteproblems: Satz
- Die Nicht-Semientscheidbarkeit des Komplements des Halteproblems: Informell
- Die Nicht-Semientscheidbarkeit des Komplements des Halteproblems: Formal
Halteproblem
Die Sprache des Halteproblems und des speziellen Halteproblems
Die SpracheDie Sprache
Satz: Das Halteproblem ist unentscheidbar
Die Sprache H des Halteproblems ist unentscheidbar, d.h. es gibt keine Turingmaschine die H entscheidet.Informeller Beweis des Halteproblems mittels Halteproblemtabelle
Wir erstellen eine Tabelle.- Auf der x-Achse tragen wir jede mögliche Eingabe auf, die ein Algorithmus haben kann.
- Auf der y-Achse tragen wir alle möglichen Algorithmen auf13.
- ,,JA'': Wenn der angegebene Algorithmus für die Eingabe terminiert.
- ,,NEIN'': Wenn der angegebene Algorithmus für die Eingabe nicht terminiert, d.h endlos läuft.
- Der Algorithmus terminiert, also ein ,,JA'' dort steht, muß er endlos laufen.
- Der Algorithmus endlos läuft, also ein ,,NEIN'' dort steht, muß er verwerfen.
Das Halteproblem ist Semientscheidbar
Wir können eine universelle TuringmaschineSpezielles Halteproblem
Die Sprache ![]() des speziellen Halteproblems lautet:
des speziellen Halteproblems lautet:
Definitionen:
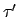 ist die DTM von der angenommen wird, daß sie die Sprache
ist die DTM von der angenommen wird, daß sie die Sprache 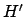 entscheidet.
entscheidet.
 ist die DTM des Halteproblemalgorithmusses:
ist die DTM des Halteproblemalgorithmusses:
- Läuft
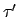 endlos, so akzeptiert
endlos, so akzeptiert  .
.
- Akzeptiert
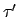 , so läuft
, so läuft  endlos.
endlos.
- Läuft
1.Fall:
|
|
|
|
|
|
|
|
|
| Widerspruch! |
2.Fall:
|
|
|
|
|
|
|
|
|
| Widerspruch! |
Reduktion
L heißt auf K reduzierbar (![]() ), wenn es eine Funktion
), wenn es eine Funktion ![]() gibt, so daß gilt
gibt, so daß gilt
d.h. daß es eine totale Übergangsfunktion gibt, die aus jeder Eingabe für L eine Eingabe für K macht und daß L und K für die gleiche (für K vorher transformierte) Eingabe akzeptieren, verwerfen oder endlos laufen.
- Ein Algorithmus für L wird erstellt, indem ein Algorithmus K benutzt wird.
- Weiterhin kann auch L als ein Spezialfall von K betrachtet werden. Dies ist keine Reduktion mehr, sondern eine Einbettung in das Problem K.
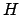 wird mit Hilfe von
wird mit Hilfe von 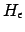 gelöst (
gelöst (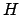 wird so umgeformt, daß es
wird so umgeformt, daß es 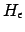 ist):
ist):
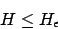
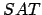 wird auf
wird auf 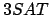 reduziert. Der
reduziert. Der 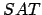 Algorithmus wird mit Hilfe von
Algorithmus wird mit Hilfe von 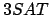 gelöst. Jede aussagelogische Formel in
gelöst. Jede aussagelogische Formel in 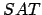 kann in eine aussagelogische Formel in
kann in eine aussagelogische Formel in 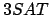 mit dem selben ,,Output'' überführt werden:
mit dem selben ,,Output'' überführt werden:
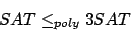
- Das spezielle Halteproblem wird in das allgemeine Halteproblem eingebettet. Hiermit zeigen wird, daß auch das allgemeine Halteproblem unentscheidbar ist.
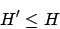
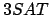 wird auf
wird auf 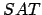 zurückgeführt.
zurückgeführt. 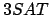 ist ein Spezialfall von
ist ein Spezialfall von 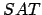 . Somit gilt diese polynomielle Reduktion, da wir sogar überhaupt gar keine Umformung durchführen müssen.
. Somit gilt diese polynomielle Reduktion, da wir sogar überhaupt gar keine Umformung durchführen müssen.
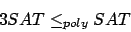
Reduktionsprinzip
K entscheidbar
K semientscheidbar
K unentscheidbar
Unentscheidbarkeit des Halteproblems
Wir zeigen, daß das spezielle Halteproblem auf das Halteproblem reduzierbar istin das allgemeine Halteproblem überführen (da die DTM
ist unentscheidbar.
Die Nicht-Semientscheidbarkeit des Komplements des Halteproblems: Satz
Die Spracheist nicht semientscheidbar.
Die Nicht-Semientscheidbarkeit des Komplements des Halteproblems: Informell
- Zunächst beinhaltet die Komplementsprache
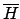 auch alle Worte, die nicht der Form
auch alle Worte, die nicht der Form 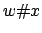
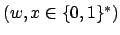 sind. Diese schließen wir jedoch aus.
sind. Diese schließen wir jedoch aus.
- Das spezielle Halteproblem war unentscheidbar (haben wir bewiesen), d.h. daß es keine DTM gibt, die H' entscheidet, mit anderen Worten, es gibt keine DTM, die alle Wörter
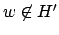 verwirft.
verwirft.
- Das Komplement des speziellen Halteproblems ist noch schärfer. Da das Verhalten der DTM17 genau umgedreht sein muß, ist es nicht sicher, ob die DTM alle Wörter
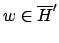 akzeptiert.
akzeptiert.
Die Nicht-Semientscheidbarkeit des Komplements des Halteproblems: Formal
AngenommenUnsere DTM
Sei
Wir setzen weiterhin
|
|
|
|
|
|
|
|
Berechnung für |
|
|
|
|
|
|
Fußnoten
- ... auf13
- Jeder Algorithmus ist formulierbar in endlich vielen Programmzeilen.
- ... auftaucht14
- Der Halteproblemalgorithmus ist ein Algorithmus und in der Tabelle sind alle Algorithmen aufgelistet.
- ... laufen15
- In der Tabelle müßten ein ,,J'' und ein ,,N'' gleichzeitig stehen.
- ... ist16
- Wir machen hier nicht den Rückschluß, daß man ein unbekanntes Problem L auf ein bekanntes Problem K zurückführt, sondern wir sehen das spezielle Halteproblem als einen Spezialfall des Halteproblems an. Deshalb schreiben wir
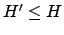 , obwohl H eigentlich noch gar nicht bekannt ist.
, obwohl H eigentlich noch gar nicht bekannt ist.
- ... DTM17
- Diese gibt es eigentlich gar nicht, aber wir nehmen einfach mal an, daß es sie gibt.