Unterabschnitte
Rekursiv aufzählbar
Rekursiv aufzählbar heißt, daß entweder die Sprache leer ist, oder daß es ein Verfahren gibt, welches die Sprache komplett aufzählt. Dabei können einzelne Elemente mehrfach aufgezählt werden.
Das Semientscheidungsverfahren kann man folgendermaßen auf die rekursive Aufzählbarkeit zurückführen: Wenn man fragt, ob ein Wort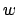 in der Sprache enthalten ist, so kann man das Aufzählungsverfahren durchlaufen lassen. Wenn das Wort enthalten ist, so berechnet das Aufzählungsverfahren irgendwann das Wort. Dann können wir ,,JA'' zurückgeben. Andernfalls läuft das Aufzählungsverfahren endlos und es wird eben halt nicht abgebrochen.
in der Sprache enthalten ist, so kann man das Aufzählungsverfahren durchlaufen lassen. Wenn das Wort enthalten ist, so berechnet das Aufzählungsverfahren irgendwann das Wort. Dann können wir ,,JA'' zurückgeben. Andernfalls läuft das Aufzählungsverfahren endlos und es wird eben halt nicht abgebrochen.
Semientscheidbar
Die Sprache wird mit Hilfe des Semientscheidungsverfahrens rekursiv aufgezählt. Wir laufen allerdings in das Problem, daß, wenn für ein Wort 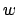 , daß nicht in der Sprache enthalten ist, das Semientscheidungsverfahren nicht terminiert, die Sprache nicht weiter aufzählt wird und der Algorithmus dann an dieser Stelle ,,hängt''.
, daß nicht in der Sprache enthalten ist, das Semientscheidungsverfahren nicht terminiert, die Sprache nicht weiter aufzählt wird und der Algorithmus dann an dieser Stelle ,,hängt''.
Wir bedienen uns hierfür eines kleinen Tricks:
Wir stellen an das Semientscheidungsverfahren die Frage, ob nach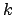 Schritten, die DTM, die semientscheidet, akzeptiert. Wenn nach
Schritten, die DTM, die semientscheidet, akzeptiert. Wenn nach 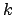 Schritten nicht akzeptiert wird, brechen wir einfach ab. Wir benutzen eine Funktion
Schritten nicht akzeptiert wird, brechen wir einfach ab. Wir benutzen eine Funktion
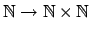 , die alle Tupel
, die alle Tupel 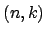 aufzählt und zwar so, daß
aufzählt und zwar so, daß 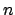 und
und 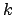 gleichmäßig erhöht werden. Beispielsweise folgendermaßen12:
gleichmäßig erhöht werden. Beispielsweise folgendermaßen12:
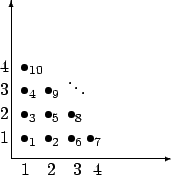
Die Zahlen an den Punkten geben hierbei die Reihenfolge an, mit der die Punkte ,,besucht'' werden. Die x-Achse kann beispielsweise 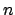 sein, die y-Achse
sein, die y-Achse 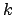 . Wir erhalten bei diesem Verfahren beispielweise die Paare
. Wir erhalten bei diesem Verfahren beispielweise die Paare
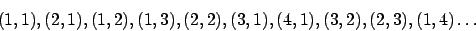
Nun bekommen wir für jedes Wort, welches in der Sprache enthalten ist, irgendwann ein ,,JA'', da die DTM ja nach endlich vielen Schritten (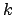 ) akzeptieren muß. Wir bekommen dann danach mehrmals für dieses Wort ein ,,JA'' und können es in die Sprache einreihen. Dies ist aber egal, da die Worte ja auch mehrmals auftreten dürfen.
) akzeptieren muß. Wir bekommen dann danach mehrmals für dieses Wort ein ,,JA'' und können es in die Sprache einreihen. Dies ist aber egal, da die Worte ja auch mehrmals auftreten dürfen.
Rekursive Aufzählbarkeit
Rekursiv aufzählbar  Semientscheidbar
Semientscheidbar
Rekursiv aufzählbar heißt, daß entweder die Sprache leer ist, oder daß es ein Verfahren gibt, welches die Sprache komplett aufzählt. Dabei können einzelne Elemente mehrfach aufgezählt werden.
Das Semientscheidungsverfahren kann man folgendermaßen auf die rekursive Aufzählbarkeit zurückführen: Wenn man fragt, ob ein Wort
Semientscheidbar  Rekursiv aufzählbar
Rekursiv aufzählbar
Die Sprache wird mit Hilfe des Semientscheidungsverfahrens rekursiv aufgezählt. Wir laufen allerdings in das Problem, daß, wenn für ein Wort Wir bedienen uns hierfür eines kleinen Tricks:
Wir stellen an das Semientscheidungsverfahren die Frage, ob nach

Nun bekommen wir für jedes Wort, welches in der Sprache enthalten ist, irgendwann ein ,,JA'', da die DTM ja nach endlich vielen Schritten (
Fußnoten
- ... folgendermaßen12
- Dieses Verfahren ist das Verfahren zum Beweis, daß die rationalen Zahlen abzählbar sind.