Unterabschnitte
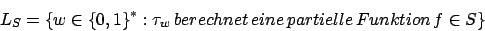
unentscheidbar.
Beweis: Wir beweisen dies, indem wir zeigen:
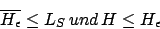
Kleine Vorbemerkung: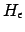 ist das Problem, ob eine Turingmaschine bei leerem Wort anhält. Dies is also ein Spezialfall des Halteproblems.
ist das Problem, ob eine Turingmaschine bei leerem Wort anhält. Dies is also ein Spezialfall des Halteproblems.
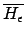 ist das Komplementproblem. Alle Codewörter
ist das Komplementproblem. Alle Codewörter
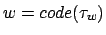 , bei der die Turingmaschine
, bei der die Turingmaschine 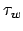 bei der Eingabe
bei der Eingabe 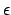 nicht anhält, sind in der Sprache enthalten.
nicht anhält, sind in der Sprache enthalten.
Jetzt geht's los: Wir führen nur den Fall aus, daß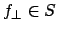 .
.
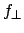 ist die Funktion, die überall undefiniert ist.
ist die Funktion, die überall undefiniert ist.
1.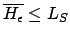 :
:
Wir wählen eine beliebige Funktion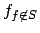 , die nicht in
, die nicht in 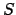 liegt.
Wir definieren eine Funktion
liegt.
Wir definieren eine Funktion 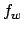 folgendermaßen:
folgendermaßen:
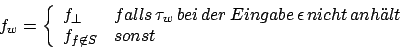
Um die Funktion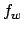 zu berechnen, simulieren wir zuerst
zu berechnen, simulieren wir zuerst 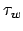 . Wenn
. Wenn 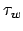 anhält, dann kann es erst weitergehen. Das Problem aber, ob
anhält, dann kann es erst weitergehen. Das Problem aber, ob 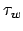 anhält ist alleine schon unentscheidbar (das beweisen wir erst weiter unten18), deshalb ist die ganze Geschichte unentscheidbar.
anhält ist alleine schon unentscheidbar (das beweisen wir erst weiter unten18), deshalb ist die ganze Geschichte unentscheidbar.
2.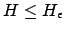 :
:
Um mit dem Halteproblem für das leere Wort das Halteproblem zu lösen, bauen wir einfach das Eingabewort für das normale Halteproblem schon in die Turingmaschine hinein. Dies können wir zum Beispiel tun, indem die Turingmaschine für das Halteproblem mit leerem Wort vorerst das Wort auf dem Band erst erzeugt. Aus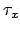 mit der Eingabe
mit der Eingabe 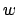 wird so
wird so 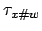 mit der Eingabe
mit der Eingabe 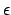 für das Halteproblem mit leerem Wort.
für das Halteproblem mit leerem Wort.
Andere unentscheidbare Probleme
Satz von Rice
Sei S eine nichtleere, echte Teilmenge der Menge aller partiellen berechenbaren Funktionen
![]() . Dann ist die Sprache
. Dann ist die Sprache
unentscheidbar.
Beweis: Wir beweisen dies, indem wir zeigen:
Kleine Vorbemerkung:
Jetzt geht's los: Wir führen nur den Fall aus, daß
1.
Wir wählen eine beliebige Funktion
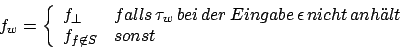
Um die Funktion
2.
Um mit dem Halteproblem für das leere Wort das Halteproblem zu lösen, bauen wir einfach das Eingabewort für das normale Halteproblem schon in die Turingmaschine hinein. Dies können wir zum Beispiel tun, indem die Turingmaschine für das Halteproblem mit leerem Wort vorerst das Wort auf dem Band erst erzeugt. Aus