Unterabschnitte
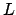 entscheidbar, dann auch
entscheidbar, dann auch 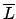 entscheidbar.
entscheidbar.
Wir benutzen eine DTM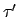 , die die DTM
, die die DTM  simuliert. Diese vertauscht die beiden Ausgaben ,,JA'' und ,,NEIN''.
simuliert. Diese vertauscht die beiden Ausgaben ,,JA'' und ,,NEIN''.
O.b.d.A. können wir annehmen, daß für alle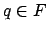 (für die DTM
(für die DTM  ) gilt
) gilt
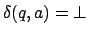
Wir definieren nun die partielle Übergangsfunktion von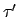 folgendermaßen:
folgendermaßen:
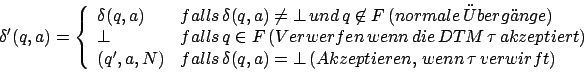
Die Endzustandsmenge von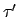 ist
ist 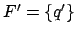 .
.
Es genügt die Implikation ,,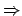 '' zu zeigen:
'' zu zeigen:
Wir nehmen die beiden Turingmaschinen, die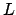 und
und 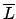 semientscheiden und schalten beide parallel. Eine der beiden Maschinen wird akzeptieren. Akzeptiert
semientscheiden und schalten beide parallel. Eine der beiden Maschinen wird akzeptieren. Akzeptiert 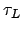 so geben wir ,,JA'' aus. Akzeptiert
so geben wir ,,JA'' aus. Akzeptiert
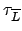 so geben wir ,,NEIN'' aus.
so geben wir ,,NEIN'' aus.
Wir können die beiden Turingmaschinen parallel schalten, indem wir eine Zweibandturingmaschine verwenden, wobei jede Turingmaschine ein Band besitzt und die Zustandsmenge11 immer hin und her schaltet.
Zusammenhang zwischen Entscheidbarkeit und Semientscheidbarkeit
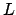 entscheidbar, dann auch
entscheidbar, dann auch 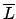 entscheidbar
entscheidbar
Wir benutzen eine DTM
O.b.d.A. können wir annehmen, daß für alle
Wir definieren nun die partielle Übergangsfunktion von
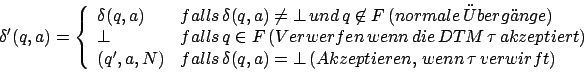
Die Endzustandsmenge von
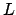 und
und 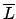 semientscheidbar
semientscheidbar
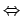
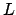 entscheidbar
entscheidbar
Es genügt die Implikation ,,Wir nehmen die beiden Turingmaschinen, die
Wir können die beiden Turingmaschinen parallel schalten, indem wir eine Zweibandturingmaschine verwenden, wobei jede Turingmaschine ein Band besitzt und die Zustandsmenge11 immer hin und her schaltet.
Fußnoten
- ... Zustandsmenge11
- Anmerkung: Die Menge der Zustände der simulierenden Gesamt-DTM beträgt:
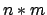 , wobei n die Menge der Zustände der ersten DTM ist und m die Menge der Zustände der zweiten DTM.
, wobei n die Menge der Zustände der ersten DTM ist und m die Menge der Zustände der zweiten DTM.