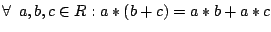Ψ Die Informatikseite

Menü
Informatik » Bachelor » Lineare Algebra » Mengen mit Verknüpfungen » Definitionen zu Mengen mit Verknüpfungen » Ring
Abelsche / kommutative Gruppe Definitionen zu Mengen mit Verknüpfungen Ring mit Einselement

Ring

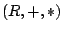
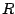
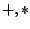
Ein Tupel $(R,+,\ast)$, wobei $R$ eine Menge und $+,\ast$ zwei Verknüpfungen

\begin{displaymath}+:R\times R\rightarrow R \,\,\,\,\,\,\,\,\,\,\,\, \ast:R\times R\rightarrow R,\end{displaymath}

heißt Ring, wenn folgende Axiome gelten:
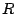
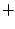
R1: $R$ zusammen mit der Addition $+$ ist eine kommutative Gruppe (Assoziativgesetz, neutrales Element, inverses Element, Kommutativgesetz)
R2: 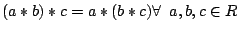$(a\ast b)\ast c= a\ast(b\ast c) \forall\,\,\,a,b,c\in R$ (Assoziativgesetz für Verknüpfung $\ast$)
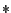R3: Es gilt (Distributivgesetze)
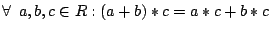
(a) $\forall\,\,\,a,b,c \in R:(a+b)\ast c=a\ast c+ b\ast c$
(b) $\forall\,\,\,a,b,c \in R:a\ast(b+c)=a\ast b+a\ast c$
Abelsche / kommutative Gruppe Definitionen zu Mengen mit Verknüpfungen Ring mit Einselement