Unterabschnitte
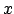 -Achse, dem Winkel um die
-Achse, dem Winkel um die 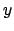 -Achse und dem Winkel um die
-Achse und dem Winkel um die 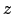 -Achse.
-Achse.
Eulerwinkel lassen sich einfach in Rotationsmatrizen umrechnen. Dazu benutze man die oben genannten Rotationsmatrizen um die jeweiligen Achsen. Die Rotationsmatritzen lassen sich konkatenieren, um eine komplexe Rotation zu erstellen. Hierbei ist jedoch zu beachten, dass die Reihenfolge der Konkatenation wichtig ist, da die Matrixmulitiplikation im allgemeinen nicht kommutativ ist.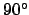 rotieren unweigerlich auf eine der anderen Koordinatenachsen. Aus dieser Koordinatenachse kann dann nicht mehr wegrotiert werden und zwei ehemals unterschiedliche Rotationen sind identisch. Beispiel:
rotieren unweigerlich auf eine der anderen Koordinatenachsen. Aus dieser Koordinatenachse kann dann nicht mehr wegrotiert werden und zwei ehemals unterschiedliche Rotationen sind identisch. Beispiel:
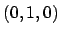 auf
auf 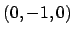 mit beidesmal derselben Orientierung:
mit beidesmal derselben Orientierung:
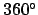 durch ,,Exponential Maps''. Folgendes Theorem besagt, dass es immer einen Gimbal-Lock bei drei Parametern geben muss:
durch ,,Exponential Maps''. Folgendes Theorem besagt, dass es immer einen Gimbal-Lock bei drei Parametern geben muss:
Theorem: Es gibt keinen Homeomorphismus5 von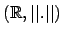 nach
nach 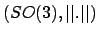 . Dies ist eine Variante des ,,Map makers dilemma''.
. Dies ist eine Variante des ,,Map makers dilemma''.
Eulerwinkel
Idee der Eulerwinkel
Um das Problem der übermäßig vielen Parameter und der Unanschaulichkeit zu beheben, kann man Eulerrotationen benutzen. Eulerrotationen werden in drei Winkeln dargestellt, nämlich dem Winkel der Rotation um dieEulerwinkel lassen sich einfach in Rotationsmatrizen umrechnen. Dazu benutze man die oben genannten Rotationsmatrizen um die jeweiligen Achsen. Die Rotationsmatritzen lassen sich konkatenieren, um eine komplexe Rotation zu erstellen. Hierbei ist jedoch zu beachten, dass die Reihenfolge der Konkatenation wichtig ist, da die Matrixmulitiplikation im allgemeinen nicht kommutativ ist.
Probleme mit Eulerwinkeln
Gimbals-Lock: Rotationen um- Rotation der
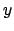 -Achse um
-Achse um 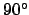 .
.
- Die
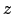 -Achse fällt nun mit der
-Achse fällt nun mit der 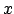 -Achse zusammen.
-Achse zusammen.
- Rotationen mit der
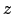 -Achse ergeben nun das gleiche Ergebnis, wie Rotationen um die
-Achse ergeben nun das gleiche Ergebnis, wie Rotationen um die 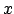 -Achse.
-Achse.
- Rotation um die
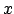 -Achse um
-Achse um 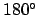 .
.
- Rotation um die
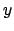 -Achse um
-Achse um 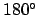 . Danach Rotation um die
. Danach Rotation um die 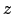 -Achse um
-Achse um 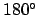 .
.
Umgehung des Gimbal-Locks
Der Gimbal-Lock ist nicht vermeidbar, allerdings verschiebbar aufTheorem: Es gibt keinen Homeomorphismus5 von
Fußnoten
- ... Homeomorphismus5
- Also bijektive, stetige Abbildung