Unterabschnitte
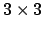 -Matrizen beschreiben. Translationen jedoch nicht. Wir können jedoch auf einfachste Weise unsere Matrix auf eine
-Matrizen beschreiben. Translationen jedoch nicht. Wir können jedoch auf einfachste Weise unsere Matrix auf eine 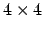 -Matrix erweitern, sowie auch
-Matrix erweitern, sowie auch 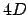 -Korridinaten verwenden und können in einem solchen System auch eine Translation darstellen. Die Verschiebung um den Vektor
-Korridinaten verwenden und können in einem solchen System auch eine Translation darstellen. Die Verschiebung um den Vektor
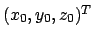 kann wie folgt dargestellt werden:
kann wie folgt dargestellt werden:
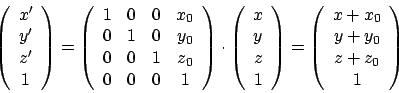
Dies ist auch schon die Schreibweise in homogenen Koordinaten.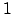 als viertes Element:
als viertes Element:
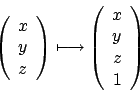
Die Überführung einer Rotationsmatrix und eines Translationsvektors in eine Matrix in homogenen Koordinaten geschieht wie folgt:
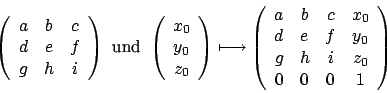
Auch eine Skalierung um einen Faktor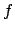 läßt sich darstellen
läßt sich darstellen
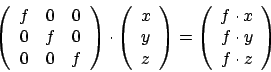
Es lassen sich auch Perspektivische Projektionen darstellen. Hier die Projektion auf die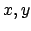 -Ebene.
-Ebene.
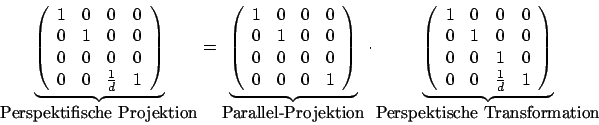
Weiterhin ist eine Textur - Interpolation möglich sowie die Linearkombination von Transformationen.
- Translation in homogenen Koordinaten
- Aufbau der homogenen Koordinaten
- Nachteile von homogenen Koordinaten und Rotationsmatrizen
Homogene Koordinaten
Translation in homogenen Koordinaten
Rotationen lassen sich mit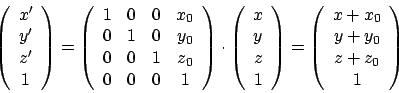
Dies ist auch schon die Schreibweise in homogenen Koordinaten.
Aufbau der homogenen Koordinaten
Ein Vektor in homogenen Koordinaten hat immer eine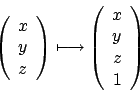
Die Überführung einer Rotationsmatrix und eines Translationsvektors in eine Matrix in homogenen Koordinaten geschieht wie folgt:
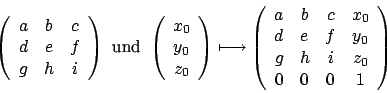
Auch eine Skalierung um einen Faktor
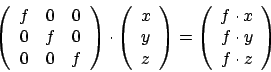
Es lassen sich auch Perspektivische Projektionen darstellen. Hier die Projektion auf die

Weiterhin ist eine Textur - Interpolation möglich sowie die Linearkombination von Transformationen.
Nachteile von homogenen Koordinaten und Rotationsmatrizen
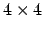 -Matritzen müssen berechnet werden.
-Matritzen müssen berechnet werden.
- Beschränkt man sich auf eine normale
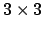 -Matrix gibt es immer noch
-Matrix gibt es immer noch 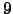 Kooridinaten für
Kooridinaten für 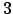 Freiheitsgerade
Freiheitsgerade
- Speicherplatzverschwendung
- Numerischer Drift
- Wenig inituitiv, auch Matritzen möglich, die gar keine Rotationsmatritzen sind, sondern etwas ganz anderes als erwünscht tun. (Wir erlauben ja alle lineare Abbildungen.)