Unterabschnitte
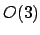 , die keine Rotationsmatrizen sind. Diese Matritzen sind die Spiegelungen und werden mit
, die keine Rotationsmatrizen sind. Diese Matritzen sind die Spiegelungen und werden mit
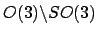 bezeichnet. Spiegelungen verletzen die erste Eigenschaft:
bezeichnet. Spiegelungen verletzen die erste Eigenschaft: 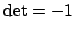
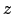 -Achse:
-Achse:
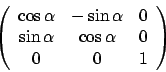
Folgende zwei Matrizen rotieren links um die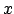 -Achse, rechts um die
-Achse, rechts um die 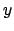 -Achse:
-Achse:

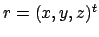 gilt für die Rotation
gilt für die Rotation 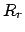 :
:
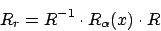
Vorgehen: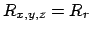 kann man allgemein aufstellen
kann man allgemein aufstellen
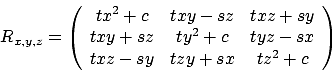
mit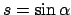 ,
,
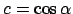 und
und
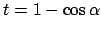 .
.
- Eigenschaften der Rotationsmatrix
- Aufbau der Rotationsmatrix
- Drehungen um beliebige Achsen mit Hilfe der Rotationsmatrix
Rotationsmatrix
Eigenschaften der Rotationsmatrix
Eine Rotation kann mit einer ![]() -Matrix dargestellt werden. Diese Matrix muss aus der Gruppe
-Matrix dargestellt werden. Diese Matrix muss aus der Gruppe ![]() kommen. Sie erfüllt folgende Eigenschaften:
kommen. Sie erfüllt folgende Eigenschaften:
- Determinante der Matrix ist
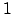 .
.
- Die Spalten bilden Einheitsvektoren einer Othonormalbasis. Die Matrix ist also aus
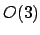 .
.
- Alle Spalten(Zeilen)-vektoren der Matrix stehen orthogonal zueinander. (logisch, da Orthonormalbasis)
- Da die Spaltenvektoren orthogonal zueinander stehen folgt, dass die transponierte Matrix das Inverse ist.
Aufbau der Rotationsmatrix
Der Aufbau der Rotationsmatrix ist wie folgt. Die folgende Matrix rotiert um die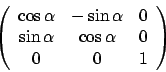
Folgende zwei Matrizen rotieren links um die

Drehungen um beliebige Achsen mit Hilfe der Rotationsmatrix
Drehungen um beliebige Achsen kann man durchführen, indem man das unbekannte Problem auf das bekannte zurückführt. Wir transformieren das Korordinatensystem, so dass wir um eine Achse drehen, drehen dann um die Achse und machen die Transformation wieder rückgängig. Für einen normierten VektorVorgehen:
- Bestimmung der Orthonormalbasis. Der erste Basisvektor ist
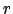 , der zweite Basisvektor
, der zweite Basisvektor 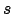 errechnet sich durch
errechnet sich durch
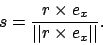
Oder falls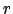 parallel zu
parallel zu 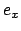 durch
durch
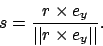
Der dritte Basisvektor ist
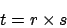
Aufstellen der Transformationsmatrix durch schreiben von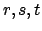 jeweils Zeilenweise in die Matrix
jeweils Zeilenweise in die Matrix 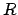 . (Spaltenweise ergibt
. (Spaltenweise ergibt 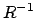 , da Orthonormalbasis)
, da Orthonormalbasis)
- Drehung durchführen.
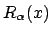 ist eine Drehung um die
ist eine Drehung um die 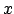 -Achse.
-Achse.
- Mit
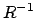 wieder zurückrechnen.
wieder zurückrechnen.
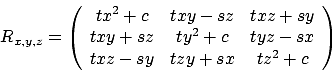
mit