Unterabschnitte
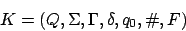
bestehend aus
Eine Konfiguration hat die Form
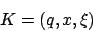
wobei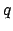 der aktuelle Zustand,
der aktuelle Zustand, 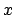 das noch zu bearbeitende Band und
das noch zu bearbeitende Band und 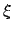 der Keller ist, wobei das oberste Kellersymbol ganz links steht und das unterste ganz rechts.
der Keller ist, wobei das oberste Kellersymbol ganz links steht und das unterste ganz rechts.
Notation der Übergangsfunktion60:
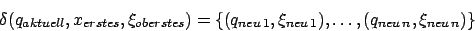
Bei einem NKA kann in mehrere Folgezustände und/oder Belegungen des Stacks überführt werden, bei DKAs ist es immer nur einer. Leider kann man die Übergangsfunktion und damit den ganzen Automaten nicht mehr zeichnen wie bei DFAs oder NFAs.
Konfigurationswechsel z.B.:
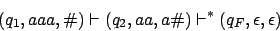
Genaueres über die Akzeptanz siehe unten.
Akzeptanz durch Endzustände:
Nach dem Lesen des kompletten Eingabewortes wird akzeptiert, wenn ein Endzustand erreicht ist. Der Kellerinhalt ist hierbei egal.
Die durch die Endzustände akzeptierte Sprache ist
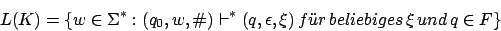
Akzeptanz durch leeren Keller:
Nach dem Lesen des kompletten Eingabewortes wird akzeptiert, wenn der Keller leer ist. Es gibt bei dieser Akzeptanzform keine Endzustände.
Die durch den leeren Keller akzeptierte Sprache ist
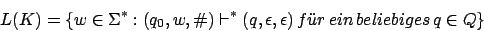
Akzeptanz durch Endzustand
Wir fügen von jedem ehemaligen Endzustand eine Übergangsfunktion mit 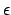 -Übergang zu dem Zustand
-Übergang zu dem Zustand 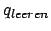 ein. Im Zustand
ein. Im Zustand 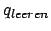 leeren wir den Keller vollständig und akzeptieren somit. Es kann sein, daß der Keller einmal während der Berechnung leer wird und wir sozusagen ausversehen akzeptieren. Deshalb fügen wir ein Kellersymbol
leeren wir den Keller vollständig und akzeptieren somit. Es kann sein, daß der Keller einmal während der Berechnung leer wird und wir sozusagen ausversehen akzeptieren. Deshalb fügen wir ein Kellersymbol 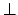 an die unterste Position des Kellers ein. Dieses entfernen wir erst, wenn wir in den Zustand
an die unterste Position des Kellers ein. Dieses entfernen wir erst, wenn wir in den Zustand 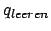 kommen. Wir benötigen dazu noch einen anderen Startzustand des NKAs, damit
kommen. Wir benötigen dazu noch einen anderen Startzustand des NKAs, damit 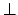 zuerst in den Keller gelegt wird und dann erst die Berechnung gestartet wird.
zuerst in den Keller gelegt wird und dann erst die Berechnung gestartet wird.
Akzeptanz durch leeren Keller
Wieder führen wir ein Symbol 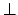 ein, welches ganz unten auf dem Stack liegt, um zu verhindern, daß der Automat vorzeitig verwirft, obwohl er eigentlich akzeptieren soll, damit wir noch die Möglichkeit haben, in einen Endzustand zu überführen. Sobald wir nun in eine Konfiguration
ein, welches ganz unten auf dem Stack liegt, um zu verhindern, daß der Automat vorzeitig verwirft, obwohl er eigentlich akzeptieren soll, damit wir noch die Möglichkeit haben, in einen Endzustand zu überführen. Sobald wir nun in eine Konfiguration
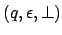 geraten, überführen wir in einen Zustand
geraten, überführen wir in einen Zustand 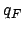 der Endzustand ist. Zuvor entfernen wir dann auch wieder
der Endzustand ist. Zuvor entfernen wir dann auch wieder 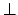 .
.
Kontextfreie Grammatik
Die Grammatik muß in Greibach-Normalform vorliegen. Die Regeln sind dann der Art:
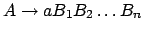 . Zu Beginn steht schieben wir das Startsymbol
. Zu Beginn steht schieben wir das Startsymbol 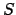 auf den Kellerspeicher. Wenn nun
auf den Kellerspeicher. Wenn nun 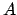 als oberstes Element auf dem Kellerspeicher steht, können wir
als oberstes Element auf dem Kellerspeicher steht, können wir
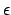 -Moves vor. Wir akzeptieren bei leerem Keller.
-Moves vor. Wir akzeptieren bei leerem Keller.
NKA
Eine NKA und eine kontextfreie Grammatik in beiden Richtungen überführbar und somit äquivalent.
reguläre Sprache
Ist 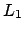 eine reguläre Sprache und
eine reguläre Sprache und 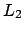 eine kontextfreie Sprache, so ist
eine kontextfreie Sprache, so ist
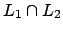 kontextfrei.
kontextfrei.
Wir können uns vorstellen, daß das Produkt eines NKAs mit einem DFA maximal ein NKA sein wird. Wir haben auch hierfür keinen Beweis gemacht.
- Definition: Nichtdeterministischer Kellerautomat (NKA)
- Konfiguration, Notation der Übergangsfunktion und Konfigurationswechsel
- Akzeptanzverhalten
- Akzeptanz durch Endzustand
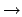 Akzeptanz durch leeren Keller
Akzeptanz durch leeren Keller
- Akzeptanz durch leeren Keller
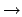 Akzeptanz durch Endzustand
Akzeptanz durch Endzustand
- Kontextfreie Grammatik
 NKA
NKA
- NKA
 kontextfreie Grammatik
kontextfreie Grammatik
- NKAs mit zwei Kellern
- reguläre Sprache
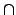 kontextfreie Sprache = kontextfreie Sprache
kontextfreie Sprache = kontextfreie Sprache
Kellerautomaten
Definition: Nichtdeterministischer Kellerautomat (NKA)
Ein NKA ist ein Tupelbestehend aus
- endlichen Menge
 von Zuständen
von Zuständen
- Eingabealphabeth
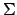
- Kelleralphabet
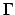
- Anfangszustand
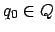
- Kellerstartsymbol
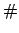 (unterstes Kellerzeichen)
(unterstes Kellerzeichen)
- Menge
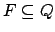 von Endzuständen
von Endzuständen
- Übergangsfunktion
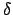
Konfiguration, Notation der Übergangsfunktion und Konfigurationswechsel
Konfiguration:Eine Konfiguration hat die Form
wobei
Notation der Übergangsfunktion60:
Bei einem NKA kann in mehrere Folgezustände und/oder Belegungen des Stacks überführt werden, bei DKAs ist es immer nur einer. Leider kann man die Übergangsfunktion und damit den ganzen Automaten nicht mehr zeichnen wie bei DFAs oder NFAs.
Konfigurationswechsel z.B.:
Genaueres über die Akzeptanz siehe unten.
Akzeptanzverhalten
Wir haben bei Kellerautomaten zwei Möglichkeiten für die Akzeptanz:Akzeptanz durch Endzustände:
Nach dem Lesen des kompletten Eingabewortes wird akzeptiert, wenn ein Endzustand erreicht ist. Der Kellerinhalt ist hierbei egal.
Die durch die Endzustände akzeptierte Sprache ist
Akzeptanz durch leeren Keller:
Nach dem Lesen des kompletten Eingabewortes wird akzeptiert, wenn der Keller leer ist. Es gibt bei dieser Akzeptanzform keine Endzustände.
Die durch den leeren Keller akzeptierte Sprache ist
Akzeptanz durch Endzustand 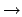 Akzeptanz durch leeren Keller
Akzeptanz durch leeren Keller
Wir fügen von jedem ehemaligen Endzustand eine Übergangsfunktion mit
Akzeptanz durch leeren Keller 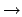 Akzeptanz durch Endzustand
Akzeptanz durch Endzustand
Wieder führen wir ein Symbol
Kontextfreie Grammatik 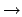 NKA
NKA
Die Grammatik muß in Greibach-Normalform vorliegen. Die Regeln sind dann der Art:
- im Wort einen nach rechts gehen, wenn das aktuelle Zeichen
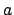 ist (ansonsten verwerfen wir)
ist (ansonsten verwerfen wir)
- und dann
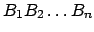 auf den Keller schieben, so daß
auf den Keller schieben, so daß 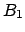 oben steht.
oben steht.
NKA 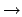 kontextfreie Grammatik
kontextfreie Grammatik
Eine NKA und eine kontextfreie Grammatik in beiden Richtungen überführbar und somit äquivalent.
NKAs mit zwei Kellern
NKAs mit zwei Kellern haben die Mächtigkeit von Turingmaschinen, da man mit einer Registermaschine mit zwei Kellern eine Turingmaschine simulieren kann. Man kann sich klar machen, daß dies auch für NKAs funktioniert, so daß NKAs eine Turingmaschine simulieren können.
reguläre Sprache 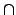 kontextfreie Sprache = kontextfreie Sprache
kontextfreie Sprache = kontextfreie Sprache
Ist Wir können uns vorstellen, daß das Produkt eines NKAs mit einem DFA maximal ein NKA sein wird. Wir haben auch hierfür keinen Beweis gemacht.
Fußnoten
- ... Übergangsfunktion60
- Das oberste Kellerelement wird immer gepoppt. Will man es auf dem Stack liegen lassen, muß man es wieder pushen. Hier kann nun
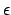 stehen, wenn es entfernt werden soll.
stehen, wenn es entfernt werden soll.