Griebach Normalform ::: Theoretische Informatik

Sei

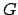eine CFG. G ist eine Griebach Normalform, falls eine Produktionen in

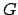von der Form

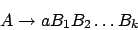
$\begin{displaymath}A\rightarrow aB_{1}B_{2}\ldots B_{k}\end{displaymath}$

wobei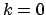

sein kann und auch 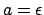$a=\epsilon$ möglich ist.

Wenn bei der Regel 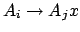$A_{i}\rightarrow A_{j}x$ das 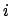größer als das 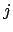ist, wird 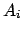$A_{i}$ überbrückt.
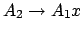
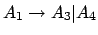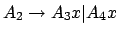$A_{2}\rightarrow A_{1}x$ $A_{1}\rightarrow A_{3}\vert A_{4}$ wird zu $A_{2}\rightarrow A_{3}x\vert A_{4}x$ .
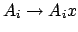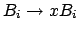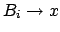Wenn die Regel der Form $A_{i}\rightarrow A_{i}x$ ist, wird diese entfernt und stattdessen $B_{i}\rightarrow xB_{i}$ und $B_{i}\rightarrow x$ eingefügt.
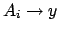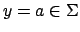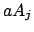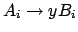Es werden für alle Regeln $A_{i}\rightarrow y$ (wobei $y=a\in\Sigma$ oder $aA_{j}$ ...) $A_{i}\rightarrow yB_{i}$ eingefügt, damit die Kette nicht zerstört wird.
Am Ende findet man dann keine linksrekursiven Regeln mehr. Alle Terminale sind nach links gerutscht.
Eliminierung der Regeln, in denen ein Terminal nicht an erster Stelle steht:
Beginn mit den größten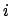 -Werten:
Für alle Regeln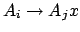 $A_{i}\rightarrow A_{j}x$ füge für alle Regeln 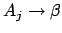$A_{j}\rightarrow\beta$ eine Regel 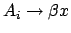$A_{i}\rightarrow \beta x$ ein und entferne die Originalregel 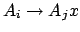$A_{i}\rightarrow A_{j}x$ . Am Ende wird kein 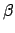$\beta$ mehr vorne steht.
Tue dasselbe wie für die A-Regeln für die B-Regeln.

Ψ Die Informatikseite