Unterabschnitte
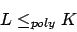
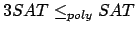 .
.
 3SAT, SAT in 3SAT Formeln umgeformt, in dem die Formel mit Hilfe der De-Morgan-Regeln verändert wird.
3SAT, SAT in 3SAT Formeln umgeformt, in dem die Formel mit Hilfe der De-Morgan-Regeln verändert wird.
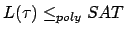 (Satz von Cook) oder
(Satz von Cook) oder
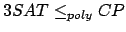 .
.
Prinzipielle Techniken für NP-Vollständigkeitsbeweise
Man halte sich vor Augen:Spezialisierung
Spezialisierung ist die einfachste Form des Nachweises. Hierbei ist das zu reduzierende Problem L ein Spezialfall des Problems K und kann in K ,,eingebettet'' werden32. Ein Beispiel hierfür istLokale Ersetzung
Die Eingabe von L wird in kleinere Einheiten von K ,,zerstückelt'' und der Algorithmus K mehrmals laufen gelassen. Beispielsweise wird bei der Reduktion33 SATTransformation mit verbundenen Komponenten
Diese Art des Beweises ist die am schwierigsten zu verstehende. Die Eingabe für K wird transformiert. Aus einer Eingabe für K entsteht also eine ganz andere Eingabe für L34. Eine solche Transfortmation ist z.BFußnoten
- ... werden32
- Diese Argumentationsweise funktioniert manchmal nicht. Mir ist es schleierhaft, warum man durch Spezialisierung polynomielle Reduzierbarkeit nachweisen kann, da zum Beispiel 2SAT auch ein Spezialfall von 3SAT ist, aber 2SAT
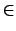 P und 3SAT
P und 3SAT 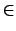 NP. 2SAT läßt sich reduzieren, indem man einfach ein Literal verdoppelt und schon hat man 3SAT. Man kann aber getrost ein Spezialproblem L auf ein Problem K reduzieren und damit die Unentscheidbarkeit zeigen.
NP. 2SAT läßt sich reduzieren, indem man einfach ein Literal verdoppelt und schon hat man 3SAT. Man kann aber getrost ein Spezialproblem L auf ein Problem K reduzieren und damit die Unentscheidbarkeit zeigen.
- ... Reduktion33
- Das sehen wir später genauer.
- ... L34
- Natürlich gibt es auch hier gewisse Transformationsregel