Unterabschnitte
Da in
in 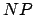 läuft ist der Berechnungsbaum für die akzeptierende Berechnung polynomiell beschränkt:
läuft ist der Berechnungsbaum für die akzeptierende Berechnung polynomiell beschränkt:
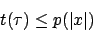
Somit ist auch die Anzahl der Bandquadrate, die besucht werden, polynomiell beschränkt. Wir müssen nur Bandquadrate betrachten, welche im folgenden Bereich sich befinden28
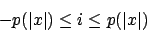
Wir setzen nun eine Formel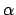 für den SAT-Algorithmus aus der Turingmaschine
für den SAT-Algorithmus aus der Turingmaschine  folgendermaßen zusammen:
folgendermaßen zusammen:
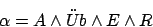
wobei
29
Anfangsbedingung A:
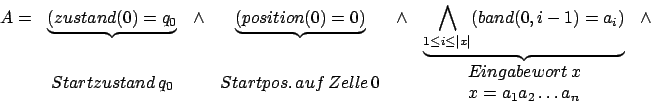
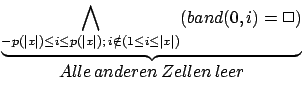
Übergangsfunktion Üb:
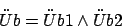
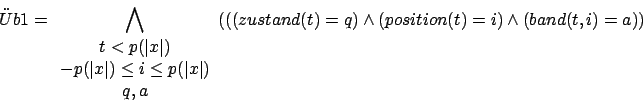
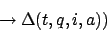
wobei
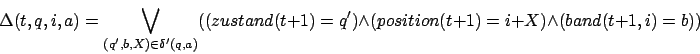
(Anmerkung: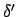 ist die neue Übergangsfunktion, die wir oben aus
ist die neue Übergangsfunktion, die wir oben aus 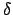 erzeugt haben.)
erzeugt haben.)
dabei ist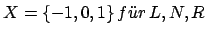
Üb2:
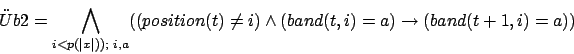
Endbedingungen:
Die Endbedingungen sagen, daß wenn ein akzeptierender Zustand erreicht wird ,,true'' zurückgegeben wird für ,,akzeptieren'':

Randbedingungen:
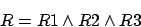
R1: Garantiert, daß zu jedem Zeitpunkt nur ein Zustand aktuell ist.
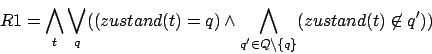
R2:31 Garantiert, daß der Schreibkopf auf genau nur einem Bandquadrat steht.
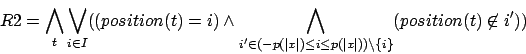
R3: Garantiert, daß zu jedem Zeitpunkt nur ein Zeichen in der Bandzelle
in der Bandzelle  steht.
steht.
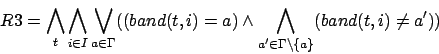
 ,,true''.
,,true''.
Die Gesamtkosten der Konstruktion sind 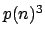 und somit polynomiell beschränkt.
und somit polynomiell beschränkt.
Satz von Cook
Satz
SAT ist NP-Vollständig
Beweis
Mittels Guess-and-Check-Methode läßt sich eine Belegung von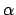 bestimmen und anschließend in polynomieller Zeit überprüfen.
bestimmen und anschließend in polynomieller Zeit überprüfen.
- Jedes NP-Problem läßt sich auf SAT in polynomiell reduzieren:
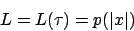
Da
Somit ist auch die Anzahl der Bandquadrate, die besucht werden, polynomiell beschränkt. Wir müssen nur Bandquadrate betrachten, welche im folgenden Bereich sich befinden28
Wir setzen nun eine Formel
wobei
| A: | Anfangsbedingungen |
| Üb: | Übergangsfunktion |
| E: | Endbedingungen |
| R: | Randbedingungen |
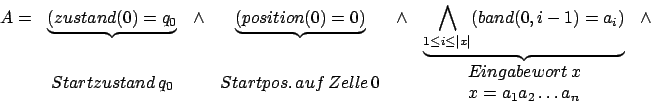
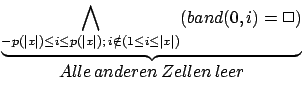
Übergangsfunktion Üb:
- Üb1: Beschreibt die Übergangsmöglichkeiten von Zeitpunkt
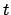 nach
nach 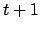 .
.
- Üb2: Sagt aus, daß alle anderen Bandzellen unverändert bleiben.
Üb1:
Wir erweitern alle verwerfenden Konfigurationen auf die Laufzeit ![]() , so daß sie uns keine Probleme mehr bereiten. Dies tun wir, indem wir in der partiellen Übergangsfunktion einen Fangzustand für alle verwerfenden Übergänge hinzufügen30.
, so daß sie uns keine Probleme mehr bereiten. Dies tun wir, indem wir in der partiellen Übergangsfunktion einen Fangzustand für alle verwerfenden Übergänge hinzufügen30.
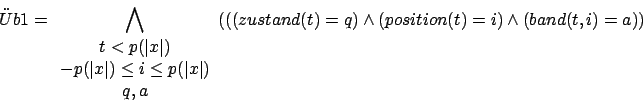
wobei
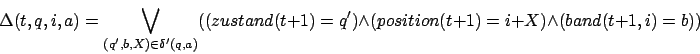
(Anmerkung:
dabei ist
Üb2:
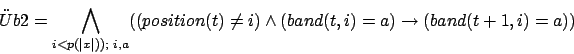
Endbedingungen:
Die Endbedingungen sagen, daß wenn ein akzeptierender Zustand erreicht wird ,,true'' zurückgegeben wird für ,,akzeptieren'':

Randbedingungen:
R1: Garantiert, daß zu jedem Zeitpunkt nur ein Zustand aktuell ist.
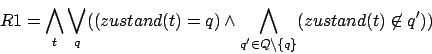
R2:31 Garantiert, daß der Schreibkopf auf genau nur einem Bandquadrat steht.
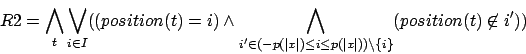
R3: Garantiert, daß zu jedem Zeitpunkt nur ein Zeichen
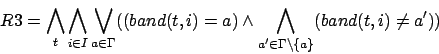
Korrektheit
Bei dieser Reduktion ,,stecken'' wir die ganze Turingmaschine in eine SAT-Formel. Wir berechnen so die ganze Turingmaschine quasi gleichzeitig. Die Berechnung geht anschaulich durch die ganzen Minterme hindurch. Wenn wir eine akzeptierende Berechnung haben, so haben wir in allen Mintermen verknüpft mitKosten
| Teil der Formel |
Kosten |
| A | |
| E | |
| Üb1 | |
| Üb2 | |
| R | |
| all in all |
|---|
Fußnoten
- ... befinden28
- Dies ist wichtig, da sonst unsere Formel
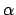 unendlich lang werden muß. Wir können also diese Beschränkung gut gebrauchen.
unendlich lang werden muß. Wir können also diese Beschränkung gut gebrauchen.
- ... 29
- Kurze Zusammenfassung der nun folgenden Definitionen:
A Stellt Anfangsbedingungen her Üb1 Die Übergangsfunktion Üb2 Alle anderen Zellen werden beim Konfigurationswechsel nicht verändert E Abbruchbedingungen R1 Immer nur ein Zustand aktuell R2 Immer nur ein Bandquadrat aktuelles R3 Immer nur ein Zeichen in einer Bandzelle - ... hinzufügen30
- Wir würden sonst mit der Teil-Formel, die wir jetzt definieren, bei einer verwerfenden Berechnung nicht terminieren, sondern weiterrechnen und vielleicht dann doch irgendwann aktzeptieren, was nicht geht.
- ...R2:31
- R2 und R3 ähneln R1 sehr