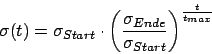Unterabschnitte
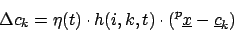
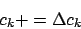
Dabei ist
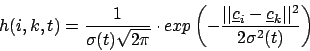
Andere wären
Für die Lernrate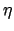 :
:
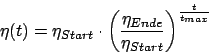
Für die Breite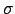 :
:
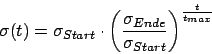
Lernregel Self Organizing Maps (SOMs)
Lernregel
Dabei ist
| Die Änderung für das Zentrum |
|
| die Lernrate in Abhängigkeit von der Zeit | |
| die Nachbarschaftsfunktion. |
|
|
|
der Abstand vom Stimulus (als Vektor!!) |
Nachbarschaftsfunktion
Die Nachbarschaftsfunktion ist zum Beispiel die Gaussglocke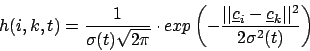
Andere wären
- Eine andere Gaussglocke:
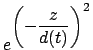
- Ein Zylinder:
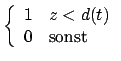
- Ein Kegel:
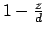
- Eine Halbwelle:
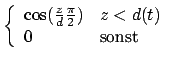
- Ein Mexican Hat
Veränderung der Lernrate mit der Zeit
Es ist sinnvoll mit der Zeit das Netz erstarren zu lassen, indem wir die Lernrate oder die Breite der Gausskurve heruntersetzen. Lassen wir das Netz erstarren, stabilisiert sich das Gitter.Für die Lernrate
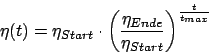
Für die Breite