Unterabschnitte
Häufen sich die Eingabebeispiele an bestimmten Stellen in diesem Raum, so ist es sinnvoll hier die Zentren zu plazieren. Wie ein solcher Eingangsraum (hier im Zweidimensionalen) beschaffen sein kann, zeigt untenstehendes Bild.
![\includegraphics[scale=0.4]{rbf-eingangsraum.eps}](img128.png)
![\includegraphics[scale=0.4]{rbf-gaussglocken.eps}](img129.png)
![\includegraphics[scale=0.4]{rbf-zufall.eps}](img130.png)
![\includegraphics[scale=0.4]{rbf-cluster.eps}](img131.png)
![\includegraphics[scale=0.4]{rbf-lvq.eps}](img132.png)
![\includegraphics[scale=0.4]{rbf-som.eps}](img133.png)
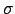 mit Hilfe einer Heuristik berechnen. Entweder
mit Hilfe einer Heuristik berechnen. Entweder
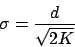
oder
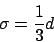
wobei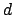 der Abstand.
der Abstand.
Anpassen bzw. Wahl der Zentren und Breiten von Radial Basis Funktionen-Netzen (RBF-Netzen)
Zentren
Die Wahl der Zentren gestaltet sich sehr schwierig. Sie ist abhängig von der Beschaffenheit des Eingangsraumes.Häufen sich die Eingabebeispiele an bestimmten Stellen in diesem Raum, so ist es sinnvoll hier die Zentren zu plazieren. Wie ein solcher Eingangsraum (hier im Zweidimensionalen) beschaffen sein kann, zeigt untenstehendes Bild.
![\includegraphics[scale=0.4]{rbf-eingangsraum.eps}](img128.png)
--
Wir können nun den Eingangsraum mit Zentren parkettieren, d.h. wir legen ihn gleichmäßig mit Zentren aus. Unten in der Grafik sehen wir feste Grenzen für die Gaussglocken. Zu beachten ist aber, dass die Gaussglocken, die wir hier von oben sehen, keine festen Grenzen haben. Geht man auf höhere Dimensionen, so wird die Parkettierung mit Gaussglocken immer schwieriger. Die Gaussglocken-Anzahl nimmt enorm zu, weshalb dieses Verfahren ein schlechtes Verfahren ist.
![\includegraphics[scale=0.4]{rbf-gaussglocken.eps}](img129.png)
--
Wir können auch Zentren durch den Zufall aus den vorhandenen Trainingsdaten auswählen. Das ist zwar leicht zu implementieren, meistens klappt diese zufällige Auswahl jedoch sehr schlecht.
![\includegraphics[scale=0.4]{rbf-zufall.eps}](img130.png)
--
Wir können vorher eine Clusteranalyse machen. Die Cluster-Analyse hat jedoch den Nachteil, dass man am Anfang nicht weiß, wieviele Cluster man hat, was man aber dem Verfahren sagen muss. Auch auf höherdimensinalen Räumen versagt das Clustering-Verfahren.
![\includegraphics[scale=0.4]{rbf-cluster.eps}](img131.png)
-----
Wir können die Zentren mit Hilfe von LVQ (Lernende Vector Quantisation) an den richtigen Ort schieben.
![\includegraphics[scale=0.4]{rbf-lvq.eps}](img132.png)
--
Oder wir können SOMs (Self organizing maps), Neuronales Gas oder m-SOMs anwenden. Unten sind m-SOMs gezeigt.
![\includegraphics[scale=0.4]{rbf-som.eps}](img133.png)
-----
Ein Gradientenabstieg kann auch gemacht werden, ist aber ungenauer und instabil.
Breiten
Wir können die Breitenoder
wobei