Angenommen wir hätten die Zentren und die Breiten der Gaussglocken schon. Wir wollen nun ,,nur noch'' die Gewichte
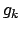
an unserem Outputneuron einstellen, so dass die Zielfunktion approximiert wird. Wir machen dies nur an einem Outputneuron. Die anderen werden analog eingestellt. Die Anzahl der Neurone ist
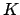
, die Anzahl der Trainingsbeispiele ist
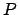
:
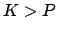 : Dieser Fall ist uninteressant. Wir können die Gewichte auf viele unterschiedliche Arten einstellen. Dieser Fall ist auch selten, da wir im Allgemeinen mehr Trainingsmuster haben, als Neuronen.
: Dieser Fall ist uninteressant. Wir können die Gewichte auf viele unterschiedliche Arten einstellen. Dieser Fall ist auch selten, da wir im Allgemeinen mehr Trainingsmuster haben, als Neuronen.
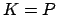 : Für den Output des Netzes haben wir folgende
: Für den Output des Netzes haben wir folgende 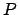 Gleichungen
Gleichungen
In Matrixschreibweise ergibt dies
Wir stellen dieses Gleichungssystem um, indem wir die Abbildung
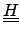 invertieren und erhalten für
invertieren und erhalten für 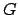 (
(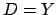 mit
mit 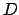 für Desired Output)
für Desired Output)
Dass die inverse Matrix existiert wird vorausgesetzt.
Praktisch gesehen wird auch keine Matrixinversion durchgeführt, sondern es werden andere Verfahren zum Lösen großer Gleichungssysteme eingesetzt.
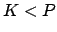 : Der eigentlich interessante Fall: Es gibt viel mehr Muster als Neurone. Es gibt mehrere Möglichkeiten die Gewichte anzupassen:
: Der eigentlich interessante Fall: Es gibt viel mehr Muster als Neurone. Es gibt mehrere Möglichkeiten die Gewichte anzupassen:
- Wir stellen wieder folgende Gleichung auf
Nun haben wir aber ein Problem beim Invertieren, dass wir die Matrix 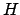 nicht invertieren können, da sie nicht quadratisch ist16. Wir weichen aus auf eine Pseudoinverse, die Moore-Penrose Pseudoinverse, die berechnet wird durch
nicht invertieren können, da sie nicht quadratisch ist16. Wir weichen aus auf eine Pseudoinverse, die Moore-Penrose Pseudoinverse, die berechnet wird durch
In Dimensionen
Die Moore-Penrose Pseudoinverse wird die Fehlerquadrate minimieren.
Also haben wir wieder
Hinweis: Die Berechnung mit der Moore-Penrose Pseudoinverse wird praktisch nicht durchgeführt, da diese Matrizen sehr hohe Dimensionen haben, wenn wir viele Trainingsmuster haben.
- Wir können auch den Gewichtsvektor
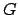 durch Lernen an Beispielen finden. Ein Gradientenabstieg ist möglich. Wir benutzen die
durch Lernen an Beispielen finden. Ein Gradientenabstieg ist möglich. Wir benutzen die 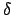 -Regel. Kein Backpropagation, da wir nur in der Outputschicht lernen müssen.
-Regel. Kein Backpropagation, da wir nur in der Outputschicht lernen müssen.
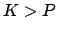 : Dieser Fall ist uninteressant. Wir können die Gewichte auf viele unterschiedliche Arten einstellen. Dieser Fall ist auch selten, da wir im Allgemeinen mehr Trainingsmuster haben, als Neuronen.
: Dieser Fall ist uninteressant. Wir können die Gewichte auf viele unterschiedliche Arten einstellen. Dieser Fall ist auch selten, da wir im Allgemeinen mehr Trainingsmuster haben, als Neuronen.
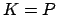 : Für den Output des Netzes haben wir folgende
: Für den Output des Netzes haben wir folgende 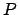 Gleichungen
Gleichungen
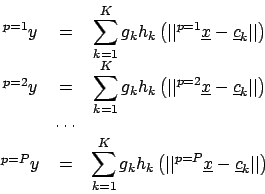
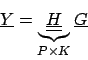
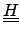 invertieren und erhalten für
invertieren und erhalten für 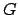 (
(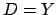 mit
mit 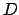 für Desired Output)
für Desired Output)
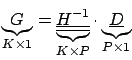
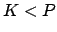 : Der eigentlich interessante Fall: Es gibt viel mehr Muster als Neurone. Es gibt mehrere Möglichkeiten die Gewichte anzupassen:
: Der eigentlich interessante Fall: Es gibt viel mehr Muster als Neurone. Es gibt mehrere Möglichkeiten die Gewichte anzupassen:
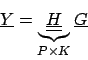
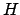 nicht invertieren können, da sie nicht quadratisch ist16. Wir weichen aus auf eine Pseudoinverse, die Moore-Penrose Pseudoinverse, die berechnet wird durch
nicht invertieren können, da sie nicht quadratisch ist16. Wir weichen aus auf eine Pseudoinverse, die Moore-Penrose Pseudoinverse, die berechnet wird durch
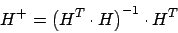
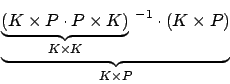
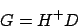
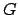 durch Lernen an Beispielen finden. Ein Gradientenabstieg ist möglich. Wir benutzen die
durch Lernen an Beispielen finden. Ein Gradientenabstieg ist möglich. Wir benutzen die 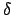 -Regel. Kein Backpropagation, da wir nur in der Outputschicht lernen müssen.
-Regel. Kein Backpropagation, da wir nur in der Outputschicht lernen müssen.