Unterabschnitte
Die Backpropagationregel führt einen Gradientenabstieg auf der Fehleroberfläche durch.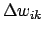 für das Gewicht
für das Gewicht 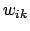 :
:
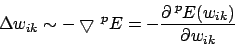
Wir führen einen Proportionalitätsfaktor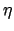 , auch Lernrate genannt, ein:
, auch Lernrate genannt, ein:
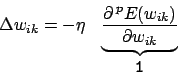
Weiterrechnen bei 1 mit mehrdimensionaler Kettenregel9
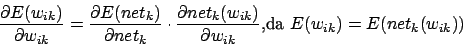
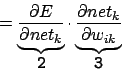
Aus 3 folgt
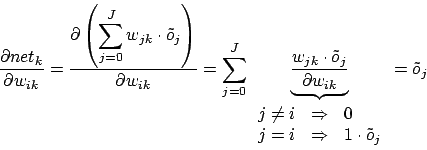
2 ist definiert als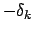 :
:
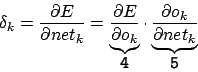
Term 5 ist abhängig von der gewählten Kennlinie des Neurons
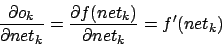
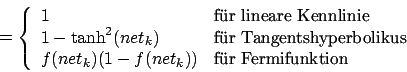
Term 4 ist abhängig von der Position des Neurons im MLP (entweder Outputlayer oder Hiddenlayer). Für das Outputlayer ist dieser Term
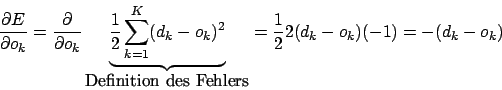
Dies führt zur Delta-Regel.
Für die darüberliegenden Layer
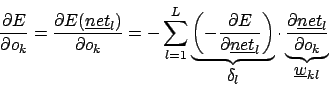
Somit ergibt sich für Backpropagation insgesamt
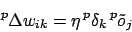
Für Outputlayer
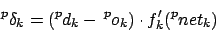
Für Hidden und Inputlayer10
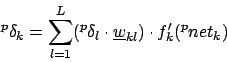
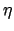 sind
sind
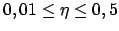 . Typisch für
. Typisch für 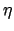 ist
ist 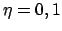 .
.
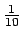 zu verkleinern. In der Lernkurve werden hier Zacken sichtbar. Der Fehler wird noch einmal geringer.
zu verkleinern. In der Lernkurve werden hier Zacken sichtbar. Der Fehler wird noch einmal geringer.
- Idee
- Herleitung
- Algorithmus
- Single-Step und Batch-Learning
- Synchrone und asynchrone Aktivierung
- Einstellen der Lernrate
- Probleme und deren Lösungen
Backpropagation of Error
Idee
Bei Netzen mit mehr Schichten wird man vor das Problem gestellt, dass man keinen direkten Fehler für Neurone der Hiddenschicht oder Schichten darüber bestimmen kann. Lange Zeit konnten deshalb mehrschichtige Netze nicht lernen. Die Backpropagation-Regel hebt jedoch dieses Dilemma auf. Sie propagiert den Fehler zurück bis zur Eingabeschicht.Die Backpropagationregel führt einen Gradientenabstieg auf der Fehleroberfläche durch.
Herleitung
Der Gradient ist die Richtung des steilsten Anstieges auf der Fehleroberfläche. Es ist ein Vektor, der uns sagt, wo es am steilsten hoch geht. Wir möchten jedoch den Fehler minimieren. Deshalb suchen wir den steilsten Abstieg. Dies ist meistens der negative Gradient. Dies muss jedoch nicht so sein. Mit dem negativen Gradienten liegen wir jedoch meistens richtig. Wir bestimmen die GewichtsänderungWir führen einen Proportionalitätsfaktor
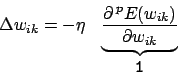
Weiterrechnen bei 1 mit mehrdimensionaler Kettenregel9
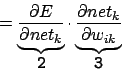
Aus 3 folgt
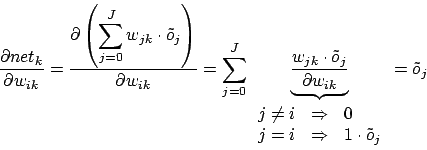
2 ist definiert als
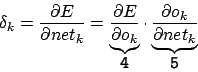
Term 5 ist abhängig von der gewählten Kennlinie des Neurons
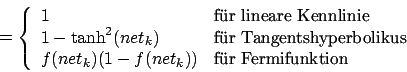
Term 4 ist abhängig von der Position des Neurons im MLP (entweder Outputlayer oder Hiddenlayer). Für das Outputlayer ist dieser Term
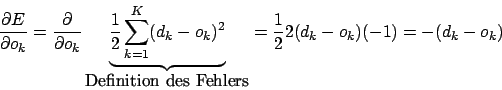
Dies führt zur Delta-Regel.
Für die darüberliegenden Layer
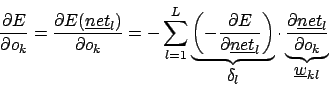
Somit ergibt sich für Backpropagation insgesamt
Für Outputlayer
Für Hidden und Inputlayer10
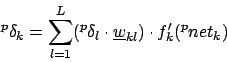
Algorithmus
| 0: | Initialisieren der Gewichte auf zufällige Werte |
|---|---|
| 1: | Trainingsmuster wählen |
| 2: | Vorwärtsschritt durchführen (den Output des neuronalen Netzes berechnen) Dabei die Aktivierungen der einzelnen Neuronen abspeichern, da wir die für die Berechnung der Ableitung der Kennlinie benötigen. |
| 3: | Desired Output mit dem tatsächlichen Output vergleichen und dadurch alle |
| 4: | Backpropagation in darüberliegende Schichten durch Berechnen aller |
| 5: | Update der Gewichte |
| 6: | Wenn nicht zufrieden, noch einmal bei 1 anfangen |
Single-Step und Batch-Learning
- Das mathematisch korrektere Verfahren ist das Batchlearning. Beim Batchlearning werden alle Muster dem Netz nacheinander zugeführt und für jedes Muster die Gewichtsänderungen festgestellt. Nachdem alle Muster dran waren, werden die Gewichtsänderung für ein Gewicht zusammenaddiert und auf das aktuelle Gewicht draufaddiert:
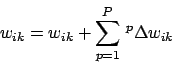
Dieses Verfahren verschlingt viel Rechenzeit. - Das schnellere Verfahren ist das Single-Step Verfahren. Es wird auch stochastisches Gradientenverfahren genannt. Hierbei berechnen wir den Fehler für ein Muster und aktualisieren nach der Hochpropagierung die Gewichte sofort. Verwirrend ist, dass nicht alle Muster dieselbe Fehleroberfläche haben11. Dieses Verfahren hat die Idee, dass alle Muster den Fehler in einer gemeinsamen Senke wohl schon minimieren werden. Wegen dieser ungefähren wagen Behauptung ist es mathematisch ungenau. Die Praxis aber zeigt, dass dies genau der Fall ist. Deshalb kommt dieses Verfahren, vor allen Dingen wegen der erhöhten Geschwindigkeit, in Anwendungen häufig zum Einsatz.
Synchrone und asynchrone Aktivierung
- Bei synchroner Aktivierung werden alle Neuronen gleichzeitig auf neue Outputwerte gesetzt. Dies kann man zum Beispiel in Spezialhardware erreichen oder man speichert die neue Ausgabe zwischen, wobei aber für jedes Neuron ein weiterer Speicherplatz verbraucht wird.
- Bei asynchroner Aktivierung wird jedes Neuron nach seiner Berechnung sofort auf die neue Ausgabe gesetzt. Bei der asynchronen Aktivierung muss man sich überlegen, wie man die Neuronen, die neu aktiviert werden, aussucht. Es gibt
- feste Reihenfolge: Es ist nur eine Reihenfolge der Neuronen möglich. Nicht vorteilhaft, da es sehr schnell zu Oszillationen auf der wechselnden Fehleroberfläche kommen kann.
- zufällige Auswahl: Man weiß nicht, wann eine Phase zuende ist. Es gibt eine kleine Wahrscheinlichkeit, mit welcher ein Neuron nie upgedatet wird.
- zufällige Permutation: Hier wird jedes Neuron upgedatet, allerdings ist die Reihenfolge zufällig gewählt. Wohl am vorteilhaftesten.
- topologische Sortierung: Bei einfachen Feed-Forward-Netzes - wie das MLP - können wir eine topologische Sortierung wählen. Wir rechnen die Neuronen der einzelnen Schichten neu. Wenn eine Schicht fertig ist, kommt von oben nach unten die nächste Schicht dran.
Einstellen der Lernrate
Gute Werte für- Eine zu hohe Lernrate verursacht, dass wir über Schluchten hinwegspringen und dass wir Oszillation in Schluchten haben.
- Eine zu kleine Lernrate verursacht, dass wir auf Plateaus verschmachten und endlos lange lernen. Des weiteren muss man bei zu kleiner Lernrate generell lange lernen.
- Allerdings sollte man die Lernrate nicht vom Fehler abhängig einstellen, da es so sein kann, dass wir auf der Fehleroberfläche auf einem Plato stecken bleiben.
- Man sollte sie auch nicht von der Zeit abhängig machen. Es kann so sein, dass die Lernkurve super aussieht, wir aber in Wirklichkeit irgendwo auf halber Strecke liegen bleiben, obwohl wir noch weiterlernen könnten.
Für Neuronen mit linearer Kennlinie benötigen wir generell eine kleinere Lernrate als für solche mit sigmoider Kennlinie:
- Bei einer sigmoiden Kennlinie können wir Pech haben und wir sind mit den vorinitialierierten Werten genau auf der falschen Seite. Beim Drehen an den Gewichten ändert sich der Fehler nur sehr langsam. Haben wir dazu noch eine kleine Lernrate, braucht Lernen ewig. (siehe dazu auch Flat-Spot-Elimination-Verfahren)
- Bei einer linearen Kennlinie können wir auf dieser sehr schnell hin und her rutschen. Um dies nicht allzu heftig zu tun, wählen wir eine kleinere Lernrate.
Probleme und deren Lösungen
- Laufen in ein Nebenminimum: Dies ist ein großes Problem neuronaler Netze. Es kann sein, dass auf ein Nebenminimum hin optimiert wird, statt auf das globale Minimum zu optimieren.
- Abhilfe verschafft hier, dass man das Netzwerk mit mehreren unterschiedlichen zufällig erzeugten Startwerten lernen läßt. Liefern alle dasselbe Ergebnis, so ist dies höchstwahrscheinlich das globale Minimum.
- Weiterhin kann man simulated annealing anwenden. Hierbei wird eine Temperatur definiert, die langsam abkühlt und die Lernrate steuert. Zu Beginn werden noch große Sprünge über die gesamte Fehleroberfläche erlaubt, so dass Nebenminima übersprungen werden. Wenn das Lernen weiter fortgeschritten ist, wird immer weiter abgekühlt, bis das Netz letztendlich in das globale Minimum läuft. Wichtig hierbei ist, dass man die Lernrate nicht abhängig vom Fehler oder der Gewichtsänderung macht.
- Parallele Änderung der Gewichte: Wir müssen die Gewichte mit unterschiedlichen zufällig gewählten Werten initialisieren. Diese sollten in der Nähe von
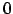 liegen, damit die Sigmoide Kennlinie sich für eine Seite entscheiden kann, ohne endlos zu rechnen. Diese Werte müssen des weiteren verschieden voneinander sein. Wenn sie nicht verschieden sind, dann passiert es, dass das Backpropagation-Verfahren auf allen Neuronen einer Schicht das Gleiche macht. Symmetrie Breaking
liegen, damit die Sigmoide Kennlinie sich für eine Seite entscheiden kann, ohne endlos zu rechnen. Diese Werte müssen des weiteren verschieden voneinander sein. Wenn sie nicht verschieden sind, dann passiert es, dass das Backpropagation-Verfahren auf allen Neuronen einer Schicht das Gleiche macht. Symmetrie Breaking
- Flat Spot Elimination: Wenn wir weit links oder weit rechts auf der Kennlinie einer sigmoiden Funktion sind, dann brauchen wir endlos lange, um daraus wieder herauszukommen. Wenn wir bei der Initialisierung gerade auf der falschen Seite angefangen haben, dann haben wir Pech gehabt. Abhilfe verschafft hier die Flat Spot Elimination. Es wird auf die Ableitung der Kennlinie ein Wert aufaddiert, welcher die Kennlinie kippt, so dass auch weit Links und weit Rechts gelernt wird.
- Oszillation: Das Netzwerk kann in Schluchten anfangen zu oszillieren, d.h. es springt immer von einer Seite zur anderen Seite der Schlucht, nimmt aber nie das Minimum an. Dies kann man verhindern, indem man immer eine andere zufällige Permutation der Trainingsmuster verwendet. Benutzt man immer die gleiche Sequenz, kann es sein, dass das Netzwerk immer dasselbe macht.
- Steckenbleiben auf flachen Plateaus: In Minima und in Maxima ist der Gradient
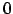 . Wenn wir ein flaches Plateau haben, wo der Gradient nur einen kleinen Betrag hat, kann es sein, dass man auf diesem Plateau steckenbleibt.
. Wenn wir ein flaches Plateau haben, wo der Gradient nur einen kleinen Betrag hat, kann es sein, dass man auf diesem Plateau steckenbleibt.