Definition der Determinante
Die Determinate ordnet jeder MatrixDie Abbildung hat die folgenden Eigenschaften
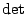 ist linear in jeder Zeile. Das bedeutet, dass wenn man aus der Matrix
ist linear in jeder Zeile. Das bedeutet, dass wenn man aus der Matrix 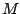 eine Zeile wegläßt und durch einen Vektor
eine Zeile wegläßt und durch einen Vektor 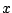 ersetzt, dass sich dann die Abbildung bezüglich dieses Vektors linear verhält.
ersetzt, dass sich dann die Abbildung bezüglich dieses Vektors linear verhält.
- Ist der Zeilenrang der Matrix kleiner als die Zeilenanzahl
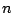 , so ist
, so ist 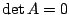 .
.
- Die Determinate der Einheitsmatrix ist
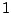 :
: 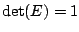 .
.