Ψ Die Informatikseite

Menü
Informatik » Bachelor » Lineare Algebra » Matrizen » Spaltenrang = Zeilenrang » Beweis: Zeilenrang = Spaltenrang
Satz: Zeilenrang = Spaltenrang Spaltenrang = Zeilenrang Inverse Matrix

Beweis: Zeilenrang = Spaltenrang

Gegeben ist eine $(m\times n)$-Matrix

\begin{displaymath}\left( \begin {array}{cccc} a_{11}&a_{12}&\cdots&a_{1n}\\ a_... ...&\vdots&\\ a_{m1}&a_{m2}&\cdots&a_{mn}\\ \end {array} \right)\end{displaymath}

Wir bezeichnen mit $R_{1},\ldots,R_{m}$ die Zeilenvektoren:

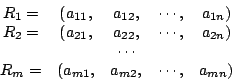
\begin{displaymath} \begin {array}{ccccc} R_{1}=&(a_{11},&a_{12},&\cdots,&a_{1n}... ...ts&\\ R_{m}=&(a_{m1},&a_{m2},&\cdots,&a_{mn})\\ \end {array} \end{displaymath}

Wenn nun der Zeilenrang $r$ ist, so haben wir $r$ linear unabhängige Vektoren, die dazu eine Basis bilden:

\begin{displaymath}S_{1}=(b_{11},b_{12},\cdots,b_{1n}), S_{2}=(b_{21},b_{22},\cdots,b_{2n}),\ldots,S_{r}=(b_{m1},b_{m2},\cdots,b_{mn})\end{displaymath}

Jeder der Zeilenvektoren $R_{i}$ ist eine Linearkombination dieser Basisvektoren:

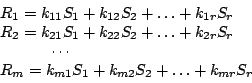
\begin{displaymath} \begin {array}{l} R_{1}=k_{11}S_{1}+k_{12}S_{2}+\ldots+k_{1r... ...{m}=k_{m1}S_{1}+k_{m2}S_{2}+\ldots+k_{mr}S_{r}\\ \end {array} \end{displaymath}

Um nun wieder jedes Element $a_{ji}$ der Matrix zu bekommen, müssen wir alle Koeffizienten, die den Zeilenvektor aus der Basis des Zeilenraumvektorraums darstellen, mit den entsprechenden Elementen der Basisvektoren multiplizieren. Für $a_{11}$ ist dies zum Beispiel

\begin{displaymath}a_{11}=k_{11}\cdot b_{11}+k_{12}\cdot b_{21}+\ldots + k_{1r}\cdot b_{r2}\end{displaymath}

Somit ist zeilenweise für alle $a_{Zeilennummer,\,\,i}$

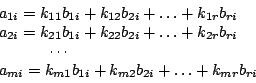
\begin{displaymath} \begin {array}{l} a_{1i}=k_{11}b_{1i}+k_{12}b_{2i}+\ldots+k_... ...=k_{m1}b_{1i}+k_{m2}b_{2i}+\ldots+k_{mr}b_{ri}\\ \end {array} \end{displaymath}

Wir können somit nun jeden Spaltenvektor folgendermaßen schreiben:

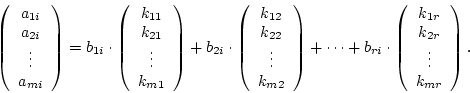
\begin{displaymath}\left( \begin {array}{c} a_{1i}\\ a_{2i}\\ \vdots\\ a_{mi}... ...} k_{1r}\\ k_{2r}\\ \vdots\\ k_{mr}\\ \end {array} \right).\end{displaymath}

Somit sind diese Vektoren Linearkombination aus $r$ Vektoren:

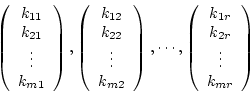
\begin{displaymath}\left( \begin {array}{c} k_{11}\\ k_{21}\\ \vdots\\ k_{m1}... ...} k_{1r}\\ k_{2r}\\ \vdots\\ k_{mr}\\ \end {array} \right) \end{displaymath}

Diese Vektoren müssen nicht zwingend linear unabhängig zueinander sein. Allerdings ist ihre Höchstzahl auf $r$ beschränkt, weshalb der
Spaltenrang 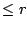$\leq r$
ist.


Man verfahre ebenso mit der transponierten Matrix und erhalte so ,,Zeilenrang $\leq r$''. Somit ist

Zeilenrang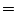$=$Spaltenrang
$\Box$

Satz: Zeilenrang = Spaltenrang Spaltenrang = Zeilenrang Inverse Matrix