Eigenschaften Untervektorraum ::: Lineare Algebra

Eigenschaften Untervektorraum

Somit hat ein Vektorraum mindestens zwei Untervektorräume. Einmal sind diese Axiome in dem Vektorraum selbst gegeben, so dass der Vektorraum Untervektorraum zu sich selbst ist. Einmal ist in jedem Vektorraum der Nullvektor enthalten. Der Nullvektor alleine ist auch ein Vektorraum.
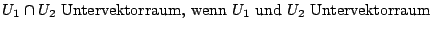
$U_{1}\cap U_{2} \mbox{ Untervektorraum, wenn } U_{1}\mbox{ und } U_{2}\mbox{ Untervektorraum}$
Sei 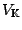$V_{\mathbb{K}}$ ein Vektorraum und 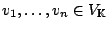$v_{1},\ldots,v_{n}\in V_{\mathbb{K}}$ . Jede Linearkombination 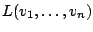$L(v_{1},\ldots,v_{n})$ ist Untervektorraum.