Ψ Die Informatikseite

Menü
Informatik » Bachelor » Lineare Algebra » Zu Beginn » Lineare Gleichungssysteme » Lösungskriterien linearer Gleichungssysteme
Zeilenstufenform einer Matrix Lineare Gleichungssysteme Weitere Lösungskriterien linearer Gleichungssysteme

Lösungskriterien linearer Gleichungssysteme

Um die Anzahl der Lösungen einer linearen Gleichung zu bestimmen, existieren Lösungskriterien:

Homogene lineare Gleichungssysteme können entweder die triviale Lösung oder mehrere Lösungen haben.

  • Triviale Lösung:
    Die triviale Lösung ist der Nullvektor; das bedeutet, dass man alle Gleichungen nur erfüllen kann, wenn man alle Variablen auf Null setzt.
    Dieser Fall tritt dann ein, wenn man das homogene lineare Gleichungssystem so auf Zeilenstufenform bringen kann, dass in jeder Zeile von oben nach unten eine Null hinzukommt und wir genausoviel Zeilen wie Spalten in der Matrix haben1.3. Beispiel für ein Gleichungssystem mit einer Matrix in Zeilenstufenform, die besagt, daß es nur die triviale Lösung gibt:

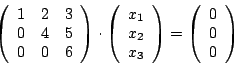
    \begin{displaymath}\left(\begin {array}{ccc}1&2&3\\ 0&4&5\\ 0&0&6\\ \end {array}... ...}\right)=\left(\begin {array}{c}0\\ 0\\ 0\\ \end {array}\right)\end{displaymath}

    Aus der letzten Zeile folgt bei diesem Gleichungssystem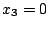 $x_{3}=0$. Dann folgt aus der zweiten Zeile 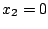$x_{2}=0$ und schließlich aus der ersten 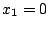$x_{1}=0$, weshalb wir nur als Lösung den Nullvektor bekommen.
    Mit einem homogenen linearen Gleichungssystem können wir testen, ob Vektoren linear abhängig oder unabhängig zueinander sind. Dabei schreiben wir die Vektoren als Spaltenvektoren in die Matrix. Hat das so gewonnene homogene lineare Gleichungssystem nur die triviale Lösung, so sind die Vektoren linear unabhängig zueinander.


  • Mehrere Lösungen: Das homogene lineare Gleichungssystem hat mehrere Lösungen, wenn es freie Variablen gibt. Eine freie Variable ist eine Variable die durch das Lösen des Gleichungssystems nicht festgelegt wird. Wir können eine solche Variable beliebig wählen und erhalten so beliebig viele Lösungen für das Gleichungssystem. Diese Lösungen spannen einen Vektorraum auf.
    Wie erkennen wir nun, ob das Gleichungssystem freie Variablen hat? Freie Variablen sind immer dann vorhanden, wenn es weniger Gleichungen im System gibt, als Variablen vorhanden sind. Beispiel:

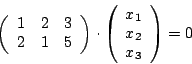
    \begin{displaymath}\left(\begin {array}{ccc}1&2&3\\ 2&1&5\\ \end {array}\right)\... ...t(\begin {array}{c}x_{1}\\ x_{2}\\ x_{3}\\ \end{array}\right)=0\end{displaymath}

    Es gibt auch lineare Gleichungssysteme, bei denen es nicht so offensichtlich ist, dass es weniger Gleichungen als Variablen gibt. Bei diesen Gleichungssystemen erkennen wir durch Bringen des Systems auf Zeilenstufenform, dass eine Nullzeile existiert. In homogenen linearen Gleichungssystemen können wir solche Nullzeilen einfach streichen (Vorsicht! Das geht nicht in inhomogenen, da wir sonst die Tatsache vernichten könnten, dass es keine Lösung gibt.). Wenn nach dem Streichen mehr Variablen als Gleichungen übrig sind, so haben wir ein Gleichungssystem mit freien Variablen.
    Kommt beim Lösen eines homogenen linearen Gleichungssystems, in welchem die Matrix aus Spaltenvektoren besteht, deren lineare Unabhängigkeit zueinander geprüft werden soll, heraus, dass dieses Gleichungssystem mehrere Lösungen hat, so sind die Vektoren linear abhängig zueinander.



Inhomogene Gleichungssysteme können keine Lösung, genau eine oder mehrere Lösungen haben:
  • Keine Lösung:
    Ein inhomogenes lineares Gleichungssystem besitzt keine Lösung, wenn die Koeffizienten einer der Gleichungen null sind, das dazugehörige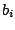 $b_{i}$ jedoch nicht null ist:

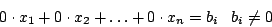
    \begin{displaymath}0\cdot x_{1}+0\cdot x_{2}+\ldots+0\cdot x_{n}=b_{i}\,\,\,\,\,b_{i}\not=0\end{displaymath}

    Eine solche Gleichung heißt entartet. Entartete Gleichungen sind nicht erfüllbar und somit ist das gesamte Gleichungssystem nicht erfüllbar, weshalb wir auch keine Lösung haben.


  • Genau eine Lösung:
    Ein inhomogenes Gleichungssystem hat genau eine Lösung, wenn das dazugehörige homogene Gleichungssystem - das dazugehörige homogene Gleichungssystem wird erzeugt, indem alle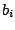 $b_{i}$ auf Null gesetzt werden - nur die triviale Lösung hat.
    Um die Lösung zu berechnen, bringen wir das inhomogene lineare Gleichungssystem auf Zeilenstufenform, wie wir es oben auch getan haben, wobei wir hier bei der Berechnung die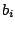 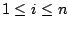$b_{i}$ ($1\leq i\leq n$) mit berücksichtigen müssen.
    Ein inhomogenes Gleichungssystem kann man dazu verwenden, um zu überprüfen, ob ein Vektor als eine Linearkombination aus anderen Vektoren erzeugt werden kann. Es gibt nämlich genau dann eine Lösung, wenn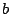 $b$ durch Linearkombination der Spaltenvektoren erzeugt werden kann. Gibt es so keine Lösung, so kann man 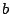$b$ nicht aus den Spaltenvektoren kombinieren. Gibt es eine oder sogar mehrere Lösungen, so geht dies.


  • Mehrere Lösungen:
    Wie bei homogenen linearen Gleichungssystemen können freie Variablen auch bei inhomogenen Systemen auftauchen. Diese existieren wieder, wenn man mehr Variablen als Gleichungen hat. Auch in inhomogenen Systemen darf man Nullzeilen streichen, wo auch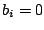 $b_{i}=0$. Allerdings darf man die entarteten Gleichungen nicht streichen.
Zeilenstufenform einer Matrix Lineare Gleichungssysteme Weitere Lösungskriterien linearer Gleichungssysteme