Unterabschnitte
Vorraussetzung für den Satz von Bayes sind,
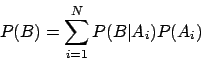
Zwei Ereignisse:
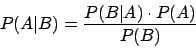
Mehr Ereignisse:
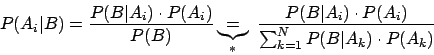
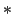 folgt mit Hilfe des Satzes der totalen W'keit.
folgt mit Hilfe des Satzes der totalen W'keit.
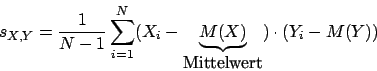
Wahrscheinlichkeitsrechnung
Satz von Bayes
Der Satz von Bayes ermöglich es sozusagen, Ursache und Wirkung zu vertauschen. Wir können feststellen, wenn ein Bestimmtes Ereignis eingetreten ist, wie groß dann die Wahrscheinlichkeit ist, dass ein spezifische Ursache der Grund dafür war.Vorraussetzung für den Satz von Bayes sind,
- Wahrscheinlichkeit für jedes Ereignis
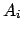 >0
>0
- Wahrscheinlichkeiten
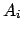 sind alle paarweise unvereinbar, d.h. ein Elementarereignis kann nicht gleichzeitig in zwei Ereignissen sein:
sind alle paarweise unvereinbar, d.h. ein Elementarereignis kann nicht gleichzeitig in zwei Ereignissen sein:
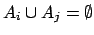 für
für 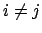 .
.
- alle Wahrscheinlichkeiten
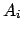 zusammen ergeben
zusammen ergeben 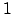 :
:
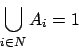
Zwei Ereignisse:
Mehr Ereignisse:
Kovarianz
- Wenn Kovarianz
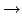 beide Zufallsvariablen wachsen gemeinsam.
beide Zufallsvariablen wachsen gemeinsam.
- Wenn Kovarianz
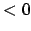
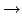 beide Zufallsvariablen fallen gemeinsam.
beide Zufallsvariablen fallen gemeinsam.
- Wenn
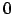 kann man eigentlich nichts sagen. Hier aber nicht weiter diskutiert.
kann man eigentlich nichts sagen. Hier aber nicht weiter diskutiert.