Unterabschnitte
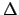 das Zeitintervall, in welchem die kontinuierliche Funktion abgetastet wird. Die Abtastrate (Samplingrate) ist das Reziproke von
das Zeitintervall, in welchem die kontinuierliche Funktion abgetastet wird. Die Abtastrate (Samplingrate) ist das Reziproke von 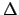 :
:
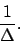
Der Wunsch ist es, aus den diskreten Abtastpunkten wieder die kontinuierliche Funktion zu erstellen. Um dies zu gewährleisten und nicht in das Aliasingproblem zu geraten, müssen wir die Ursprungsfunktion bandbreitenbegrenzen.
Mit Hilfe der Fouriertransformierten läßt sich eine Bandbreitenbegrenzung erzeugen:
Die Funktion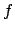 ist bandbreitenbegrenzt durch
ist bandbreitenbegrenzt durch 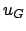 genau dann, wenn
genau dann, wenn
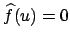 für alle
für alle 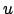 mit
mit 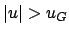 , d.h. höhere Frequenzen kommen nicht vor.
, d.h. höhere Frequenzen kommen nicht vor.
Es werden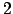 Abtastpunkte pro Periode mindestens gebraucht. Die Abtastfrequenz muss also das doppelte von
Abtastpunkte pro Periode mindestens gebraucht. Die Abtastfrequenz muss also das doppelte von 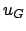 betragen.
betragen.
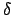 -Funktion) hat folgende Eigenschaften:
-Funktion) hat folgende Eigenschaften:
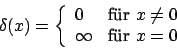
Die Fläche unter der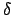 -Funktion ist
-Funktion ist 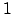 :
:
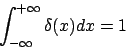
Eine konstante Funktion aus dem Ortsraum gibt die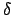 -Funktion im Frequenzraum. Ebenso umgekehrt. Eine Kammfunktion wird zu einer anderen Kammfunktion.
-Funktion im Frequenzraum. Ebenso umgekehrt. Eine Kammfunktion wird zu einer anderen Kammfunktion.
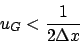
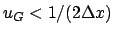 ?
?
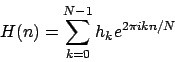
diese Formel kann durch Matrix-Vektormultiplikation implementiert werden.
inverse diskrete Fouriertransformation
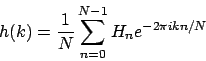
Transformation kann in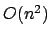 berechnet werden. Mit Schneller Fouriertransformation in
berechnet werden. Mit Schneller Fouriertransformation in 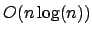 .
.
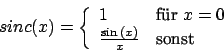
Dieser Kernel ist in Frequenzraumdarstellung die Rechteckfunktion.
Leider ist dieser Filter inpraktialbel, so dass wir auf einen nicht idealen Tiefpassfilter ausweichen müssen. Inpraktikabel ist er deshalb, weil die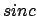 -Funktion im Unendlichen immer weiter abflacht und nicht
-Funktion im Unendlichen immer weiter abflacht und nicht 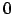 ist.
ist.
- Sampling
- Deltafunktion
- Abtasttheorem
- Tiefpassfilter
- Diskrete Fouriertransformation
- Tiefpassfilter in Frequenzraumdarstellung
- Tiefpassfilter in Ortsraumdarstellung
Diskrete Signale
Sampling
Ein zeitdiskretes Signal kann aus einem kontinuierlichen Signal durch Abtastung (Sampling) entstehen. Dabei istDer Wunsch ist es, aus den diskreten Abtastpunkten wieder die kontinuierliche Funktion zu erstellen. Um dies zu gewährleisten und nicht in das Aliasingproblem zu geraten, müssen wir die Ursprungsfunktion bandbreitenbegrenzen.
Mit Hilfe der Fouriertransformierten läßt sich eine Bandbreitenbegrenzung erzeugen:
Die Funktion
Es werden
Deltafunktion
Die Deltafunktion (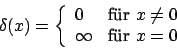
Die Fläche unter der
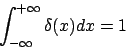
Eine konstante Funktion aus dem Ortsraum gibt die
Abtasttheorem
Das Abtasttheorem sagt aus, dass für die Nyquist-Frequenz (auch Grenzfrequenz genannt) gilt:Tiefpassfilter
Wie kann man erreichen, das- Höhere Abtastfrequenz.
- Tiefpassfilter.
Diskrete Fouriertransformation
Abbildungsvorschrift für diskrete Fouriertransformation ist gegeben durch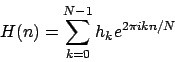
diese Formel kann durch Matrix-Vektormultiplikation implementiert werden.
inverse diskrete Fouriertransformation
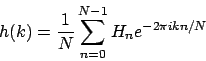
Transformation kann in
Tiefpassfilter in Frequenzraumdarstellung
- Führe insgesamt beim Abtastsignal Fouriertransformation durch.
- Multipliziere mit der Rechteckfunktion
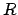 .
.
- Führe inverse Fouriertransformation durch.
Tiefpassfilter in Ortsraumdarstellung
Der FIR-Filter arbeitet nur im Ortsraum. Durchgeführt wird eine diskrete Konvolution zwischen Signal und einem ,,Filter-Kernel''. Ein idealer Tiefpassfilter hat den Kernel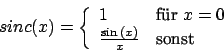
Dieser Kernel ist in Frequenzraumdarstellung die Rechteckfunktion.
Leider ist dieser Filter inpraktialbel, so dass wir auf einen nicht idealen Tiefpassfilter ausweichen müssen. Inpraktikabel ist er deshalb, weil die