Unterabschnitte
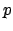 gibt, so dass gilt
gibt, so dass gilt
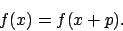
Die Periode ist nicht eindeutig, denn Vielfache von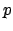 ergeben wieder Perioden.
ergeben wieder Perioden.
Beschränkte Funktionen können wir einfach zu Perioden ergänzen. Wenn die Originalfunktion stetig war, riskieren wir dabei an den Schnittstellen Unstetigkeitsstellen. Durch Strecken können wir auch auf eine Periode von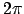 kommen.
kommen.
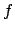 in verschiedene Frequenzen aufbricht, genauso wie ein Prisma das Licht in seine einzelnen Farbkomponenten aufbricht.
in verschiedene Frequenzen aufbricht, genauso wie ein Prisma das Licht in seine einzelnen Farbkomponenten aufbricht.
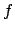 eine periodische Funktion sein. Es entsteht eine Fourierreihe, wenn man die einzelnen durch Fouriertransformation erzeugten Fourierpolynome aufeinander aufaddiert, die sich wieder der Originalfunktion
eine periodische Funktion sein. Es entsteht eine Fourierreihe, wenn man die einzelnen durch Fouriertransformation erzeugten Fourierpolynome aufeinander aufaddiert, die sich wieder der Originalfunktion 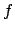 nähert.
nähert.
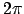 -periodischen Funktionen, welcher zusammen mit einem Skalarprodukt ein Hilbertraum ist, angeben können. Um eine periodische Fkt. dorthin zu bekommen müssen wir die Periode auf
-periodischen Funktionen, welcher zusammen mit einem Skalarprodukt ein Hilbertraum ist, angeben können. Um eine periodische Fkt. dorthin zu bekommen müssen wir die Periode auf 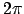 skalieren, sowie die Fkt von
skalieren, sowie die Fkt von
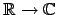 laufen lassen. Die Orthornomalbasis für diesen Funktionsraum ist nun
laufen lassen. Die Orthornomalbasis für diesen Funktionsraum ist nun
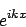
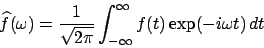
Rückgängigmachung der Fouriertransformation
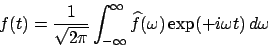
Wichtig ist, dass nur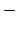 und
und 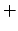 -Zeichen vertauscht werden.
-Zeichen vertauscht werden.
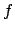 mit Hilfe ihrer Schwingungen immer weiter annähern. Hat die Funktion
mit Hilfe ihrer Schwingungen immer weiter annähern. Hat die Funktion 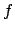 Unstetigkeitsstellen, so tritt das Gibbsche Phänomen auf:
Unstetigkeitsstellen, so tritt das Gibbsche Phänomen auf:
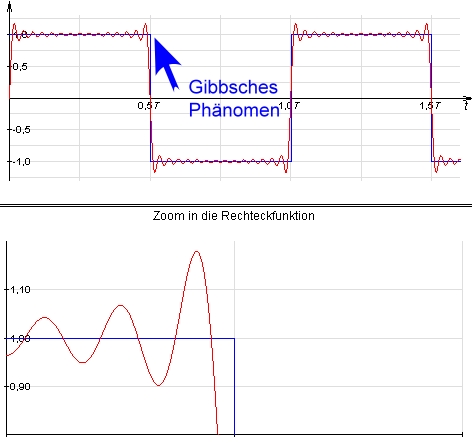
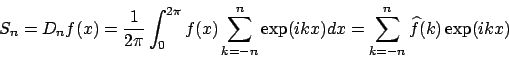
Eine andere Darstellung für die Fourierreihe ist
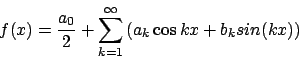
mit
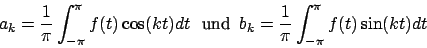
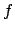 und einer gespiegelten, verschobenen Funktion
und einer gespiegelten, verschobenen Funktion 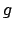 darstellt
darstellt
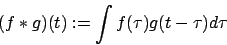
Bei der diskreten Faltung wird das Integral durch die Summe ersetzt:
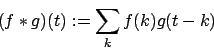
In dem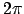 -periodischen Vektorraum kann man die Faltung wie folgt definieren
-periodischen Vektorraum kann man die Faltung wie folgt definieren
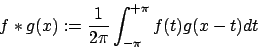
somit kann man die Fourierkoeffizienten neu definieren als
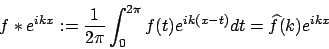
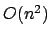 , während die schnelle Fouriertransformation (FFT für Fast Fourier Transformation) eine Laufzeit von
, während die schnelle Fouriertransformation (FFT für Fast Fourier Transformation) eine Laufzeit von 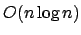 benötigt, weshalb wir eine Fouriertransformation überhaupt machen können.
benötigt, weshalb wir eine Fouriertransformation überhaupt machen können.
- Periode
- Fouriertransformation
- Orthonormalbasen im Hilbertraum
- Formeln für Fouriertransformation
- Fourierreihe
- Faltung
- Naive und schnelle Fouriertransformation
Signalverarbeitung
Periode
Eine Funktion heißt periodisch, falls es einDie Periode ist nicht eindeutig, denn Vielfache von
Beschränkte Funktionen können wir einfach zu Perioden ergänzen. Wenn die Originalfunktion stetig war, riskieren wir dabei an den Schnittstellen Unstetigkeitsstellen. Durch Strecken können wir auch auf eine Periode von
Fouriertransformation
Anschaulich: Eine Fouriertransformation ist ein mathematisches Prisma, welches eine Funktion- Die Funktion
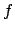 ist abhängig von der Zeit,
ist abhängig von der Zeit,
- die durch Fouriertransformation erzeugte Funktion
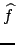 ist abhängig von der Frequenz.
ist abhängig von der Frequenz.
Orthonormalbasen im Hilbertraum
Warum kann man eine Fouriertransformation überhaupt machen? Der Grund ist, dass wir Orthornormalbasen in dem Raum derFormeln für Fouriertransformation
Erzeugnung der Fouriertransformation
Rückgängigmachung der Fouriertransformation
Wichtig ist, dass nur
Fourierreihe
Mit Hilfe der Fourierreihe läßt sich eine Funktion
Das ![]() te Fourierpolynom
te Fourierpolynom ![]() einer Funktion
einer Funktion ![]() aus einem Hilbertraum ist definiert als
aus einem Hilbertraum ist definiert als
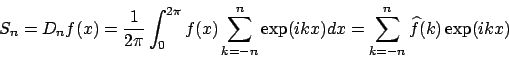
Eine andere Darstellung für die Fourierreihe ist
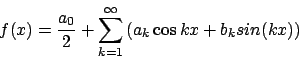
mit
Faltung
Faltung ist eine Art von Multiplikation von zwei Funktionen. Liefert eine Funktion, die die Überlappung vonBei der diskreten Faltung wird das Integral durch die Summe ersetzt:
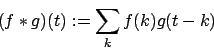
In dem
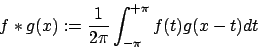
somit kann man die Fourierkoeffizienten neu definieren als