Unterabschnitte
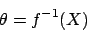
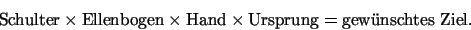
Die gewünschten Polynome werden zeilenweise extrahiert.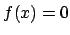 zu lösen iteriert man im eindimensionalem Fall gemäß
zu lösen iteriert man im eindimensionalem Fall gemäß
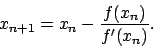
Das Verfahren konvergiert schnell. Hat aber leider das Problem, dass es für leicht konstruierbare Fälle oszilliert.
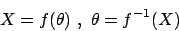
schreiben wir
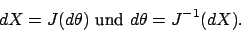
Lineares Programmierproblem in Standardform: Minimiere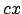 unter den Bedingungen
unter den Bedingungen
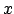 ist der Variablenvektor für die Lösung,
ist der Variablenvektor für die Lösung, 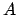 ist Matrix bekannter Koeffizienten und
ist Matrix bekannter Koeffizienten und 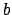 und
und 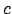 sind Vektoren mit bekannten Koeffizienten. (Hier
sind Vektoren mit bekannten Koeffizienten. (Hier 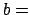 Ziel)
Ziel)
Gute Verfahren zum Lösen vorhanden. Zuerst Simplex-Verfahren mit exponentieller Laufzeit. Später auch viele Verfahren mit polynomieller Laufzeit.
Das Optimierungsproblem muss unter Einhaltung von Zwangsbedingungen gelöst werden.
Lösungsstrategie ist hier die active set strategy: Es wird ein legaler Startpunkt gewählt. Dann wird mit einer Iterationssequenz legaler Punkte an den Rändern der Zwangsbedingungen (welche Mengen darstellen) entlang Richtung Ziel konvergiert. Die aktuelle Menge an legalen Punkten wird die ,,active set'' genannt. (Siehe auch in Matlab Optimization Toolbox das Zeltstangenbeispiel)
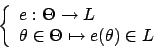
Dabei enthält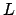 nicht nur die Informationen über die Position des Endeffektors im Raum, sondern auch Richtungsangaben. Die ersten drei Werte sind die Position. Dann kommen zwei Einheitsvektoren, die die Orientierung des Endeffektors beschreiben.
nicht nur die Informationen über die Position des Endeffektors im Raum, sondern auch Richtungsangaben. Die ersten drei Werte sind die Position. Dann kommen zwei Einheitsvektoren, die die Orientierung des Endeffektors beschreiben.
Zusätzlich werden noch sogenannte Goals definiert. Goals sind Punktmengen, die der Endeffektor erreichen soll. Es wird eine Funktion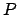 definiert, die den quadratischen Abstand in Position und Orientierung darstellt. Zhao und Badler geben die entsprechenden Formeln für einige Goals an, wie z.B. das Finden eines Punktes im Raum (hierbei ist
definiert, die den quadratischen Abstand in Position und Orientierung darstellt. Zhao und Badler geben die entsprechenden Formeln für einige Goals an, wie z.B. das Finden eines Punktes im Raum (hierbei ist 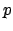 der zu findende Punkt und
der zu findende Punkt und 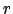 die aktuelle Koordinate:
die aktuelle Koordinate:
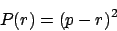
Ein Gradient läßt sich angeben mit
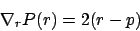
Über den Gradienten wird das Ziel immer weiter angenäher.
Ebenso verfährt er für Orientierung-Goals, Zielen-auf-Goals, Linien-Goals, Ebenen-Goals und Halbraum-Goals. Zuguterletzt wird alles mit einem Assembler zusammengesetzt und zu einem Nicht-Linearen-Gleichungssystem gemacht.
Zusätzlich müssen über eine Indexfunktion die einzelnen Constraints (Endeffektor und Goals) noch in Korospondenz zu dem Gesamtsystem gesetzt werden. (Warum, keine Ahnung)
Einzelne Constraints können über eine Gewichtsfunktion stärker gewichtet werden.
- Anwendungsgebiete
- Lösen mit Polynomgleichungen
- Iterative Verfahren
- Newton-Verfahren
- Iterative Nullstellensuche mit invertierter Jakobimatrix
- Nicht-Lineares Programmieren
- Quadratisches Programmieren
- Zhao und Badler
Inverse Kinematik
Anwendungsgebiete
- Die Inverse Kinematik wird angewandt, um dem Animateur die Möglichkeit zu geben, einen Punkt zu bestimmen, wohin dann der Endeffektor gebracht wird.
- Weiterhin wird die Inverse Kinematik benutzt, um Teilprobleme beim Editieren von Bewegungen zu lösen.
- ...
Lösen mit Polynomgleichungen
Das inverse Kinematikproblem kann auf das Lösen eines Systems von Polynomgleichungen zurückgeführt werden. Diese Polynomgleichungen erhält man, indem man die konkatenierten Matritzen der Gelenke multipliziert mit dem Ursprung dem gewünschten Ziel gleichsetzt:Die gewünschten Polynome werden zeilenweise extrahiert.
- Dabei wird für jede Winkel-Trigeometrische-Funktion-Kombination ein neues Symbol gesetzt. Also
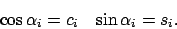
- Damit die Winkeleigenschaft erhalten bleibt wird folgende Gleichung hinzugefügt:
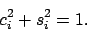
Iterative Verfahren
Um solche Probleme lösen zu können, muss man auf iterative Verfahren zurückgreifen. Im folgenden werden einige Beispiele für iterative Verfahren genannt.Newton-Verfahren
Für das Newton-Verfahren muss die Funktion differenzierbar sein. Um das ProblemDas Verfahren konvergiert schnell. Hat aber leider das Problem, dass es für leicht konstruierbare Fälle oszilliert.
Iterative Nullstellensuche mit invertierter Jakobimatrix
Durch die Iterative Suche weichen wir von den zuvor gestellten Problem ab. Wir wollen Veränderungen berechnen, die uns helfen, näher an die Lösung heranzukommen. Stattschreiben wir
- Aufstellen der Jakobimatrix. Die Jakobimatrix hat die Form
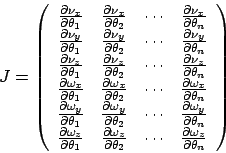
Wobei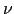 eine Position und
eine Position und 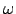 eine Orientierung.
eine Orientierung.
- Da die Jakobimatrix im allgemeinen nicht quadratisch ist, müssen wir sie mit der Moore-Penrose-Pseudoinverse invertieren. Sie ist in
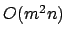 berechenbar.
berechenbar.
- Problem: Da die Pseudoinverse approximierend lokal ist, können Trackingfehler entstehen. Sobald ein Trackingfehler festgestellt wurde, muss man interpolieren.
- Problem: Singularitäten. Bei voll ausgestreckter Struktur verliert die Jakobimatrix an Rang. Man könnte die Singularitäten vorrausberechnen. Bei komplizierten Systemen ist dies aber nicht möglich.
- Problem: oszillierende Systeme wenn Position nicht erreichbar. Lösung mit Damped Least Square Methode (Gedämpfte kleinstes Quadrat) Bei dieser Methode wird minimiert:
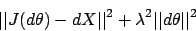
Nicht-Lineares Programmieren
Das Problem der inversen Kinematik kann als nicht-lineares Programmierproblem aufgefaßt werden. Da vielleicht eine Nullstellensuche nicht möglich, da Szenario zu komplex oder auch gar nicht erreichbar, suchen wir nur nach Minima. Dabei führen wir eine Suche nach lokalen Minimum durch. Falls dies fehlschlägt und wir dabei auch nicht gleichzeitig das globale Minimum finden, wiederholen wir das Verfahren mti einem anderen Startwert.Lineares Programmierproblem in Standardform: Minimiere
Gute Verfahren zum Lösen vorhanden. Zuerst Simplex-Verfahren mit exponentieller Laufzeit. Später auch viele Verfahren mit polynomieller Laufzeit.
Quadratisches Programmieren
Problem kann man auch mit quadratischem Programmieren lösen. Eine quadratische Gleichung soll minimiert werden. Man stößt an die Grenzen des praktisch machbaren.Das Optimierungsproblem muss unter Einhaltung von Zwangsbedingungen gelöst werden.
Lösungsstrategie ist hier die active set strategy: Es wird ein legaler Startpunkt gewählt. Dann wird mit einer Iterationssequenz legaler Punkte an den Rändern der Zwangsbedingungen (welche Mengen darstellen) entlang Richtung Ziel konvergiert. Die aktuelle Menge an legalen Punkten wird die ,,active set'' genannt. (Siehe auch in Matlab Optimization Toolbox das Zeltstangenbeispiel)
Zhao und Badler
Zhao und Badler sehen den Endeffektor wie gewohnt als eine Abbildung der einzelnen Winkel auf einen Punkt in Raum an.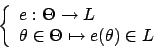
Dabei enthält
Zusätzlich werden noch sogenannte Goals definiert. Goals sind Punktmengen, die der Endeffektor erreichen soll. Es wird eine Funktion
Ein Gradient läßt sich angeben mit
Über den Gradienten wird das Ziel immer weiter angenäher.
Ebenso verfährt er für Orientierung-Goals, Zielen-auf-Goals, Linien-Goals, Ebenen-Goals und Halbraum-Goals. Zuguterletzt wird alles mit einem Assembler zusammengesetzt und zu einem Nicht-Linearen-Gleichungssystem gemacht.
Zusätzlich müssen über eine Indexfunktion die einzelnen Constraints (Endeffektor und Goals) noch in Korospondenz zu dem Gesamtsystem gesetzt werden. (Warum, keine Ahnung)
Einzelne Constraints können über eine Gewichtsfunktion stärker gewichtet werden.