Ψ Die Informatikseite

Menü
Informatik » Bachelor » Theoretische Informatik » LR(0)-Grammatiken » Eindeutigkeit von LR(0)-Grammatiken
Verbale Definition von LR(0)-Grammatik LR(0)-Grammatiken Präfixeigenschaft

Eindeutigkeit von LR(0)-Grammatiken

Jede LR(0)-Grammatik ist eindeutig.

Sei $G$ eine LR(0)-Grammatik. Zu jeder Rechtssatzform $t\not= S$ gibt es ein eindeutig bestimmtes Tupel $(x,y,z,A)$, so daß folgende Bedingungen erfüllt sind:

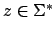  • $x,y\in(V\cup\Sigma)^{*}$ $z\in\Sigma^{*}$ und $A\in V$
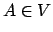
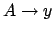  • $A\rightarrow y$ ist eine Regel in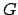 $G$
  • $t=xyz$
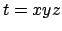
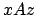  • $xAz$ ist eine Rechtssatzform
Aus der Definition der LR(0)-Bedingungen folgt, daß $A\rightarrow y$ einzigste Regel ist, um $y$ wieder rückwärts abzuleiten. Aus der Definition folgt, daß $xAz$ einzigster Griff von $(xy,y)$ ist. Somit gibt es nur einen einzigen Rückwärtsableitungspfad.
$\Rightarrow$ Jede LR(0)-Grammatik ist eindeutig

Damit ist gezeigt, daß LR(0)-Sprachen von einem deterministischen Kellerautomaten entschieden werden können.
Verbale Definition von LR(0)-Grammatik LR(0)-Grammatiken Präfixeigenschaft