Unterabschnitte
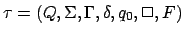 :
:
Es gibt ein Band und einen aktuellen Zustand auf den der Zeiger der Turingmaschine zeigt. Ein Raum auf dem Band heißt Bandzelle oder Bandquadrat.
Eine partielle Übergangsfunktion hat die Form
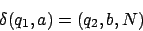
Eine Turingmaschine kann
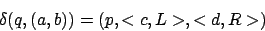
Eine Konfiguration wird wie folgt dargestellt:
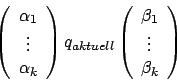
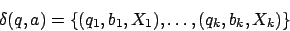
Die Konfiguration ist ein Baum.
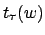 = Anzahl der Konfigurationswechsel, die
= Anzahl der Konfigurationswechsel, die  bei der Eingabe
bei der Eingabe 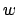 durchführt.
durchführt.
Platzkomplexität:
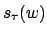 = Anzahl der Bandzellen, die
= Anzahl der Bandzellen, die  bei der Eingabe
bei der Eingabe 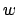 besucht.
besucht.
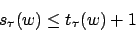
,da die Turingmaschine auch sofort abbrechen kann. In diesem Fall würden zwar eine Bandzelle besucht aber keine Zeit verbraucht werden. Es würde stehen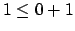 . Man sieht, daß die
. Man sieht, daß die 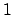 von Nöten ist.
von Nöten ist.
Die Anzahl der Konfigurationswechsel der simulierenden DTM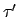 ist beschränkt durch ein konstantes Vielfaches der Anzahl der Bandquadrate, die die zu simulierende DTM
ist beschränkt durch ein konstantes Vielfaches der Anzahl der Bandquadrate, die die zu simulierende DTM  benutzt.
Es gilt:
benutzt.
Es gilt:
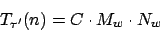
wobei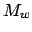 die Konfigurationswechsel der Original-DTM sind und
die Konfigurationswechsel der Original-DTM sind und 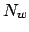 die Anzahl der Bandquadrate, die besucht wurden, sowie
die Anzahl der Bandquadrate, die besucht wurden, sowie 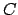 eine Konstante ist. Es folgt:
eine Konstante ist. Es folgt: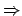
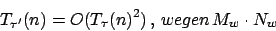
Es gilt auch
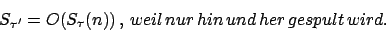
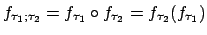
Man vereinigt beide Zustandsmengen6. Alle Endzustände der ersten DTM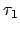 ersetzt man durch normale Zustände. Wird ein solcher Zustand erreicht, so leitet die DTM in die Zustandsmenge der zweiten DTM
ersetzt man durch normale Zustände. Wird ein solcher Zustand erreicht, so leitet die DTM in die Zustandsmenge der zweiten DTM 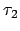 über:
über:
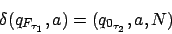
Schleifen, bedingte Anweisungen usw.
Wir konstruieren eine DTM, die die Bedingung überprüft. Abhängig von der Ausgabe dieser DTM führen wir in die eine oder die andere DTM mit Hilfe des Zustandsmengenwechsels über.
Unterprogramme
Es gibt Zustände, in denen Kontrollinformationen mitgespeichert werden (z.B. Rücksprungadressen). Lokale Variablen von Unterprogrammen können auf einem Extraband gespeichert werden. Die wirft jedoch Probleme bei der Rekursion auf. Besser ist es, sie nacheinander an Stellen des zweiten Bandes zu speichern und sie mit entsprechenden Sonderzeichen von anderen Unterprogrammvariablen zu trennen.
- Einbandige ,,normale'' Turingmaschinen (deterministisch)
- Mehrbandige Turingmaschinen
- Nichtdeterministische Turingmaschinen
- Kosten von Turingmaschinen
- Simulation von mehrbandigen Turingmaschinen durch einbandige Turingmaschinen
- Programmierung von DTMs
Turingmaschinen (kurz: DTM oder NTM)
Einbandige ,,normale'' Turingmaschinen (deterministisch)
Eine DTM (deterministische Turingmaschine4) ist ein 7er-Tupel| Q | Zustandsmenge |
| Eingabealphabet | |
| Bandalphabet | |
| partielle Übergangsfunktion, der Form
|
|
| Startzustand ( |
|
| Blanksymbol (
|
|
| Endzustandsmenge ( |
Eine partielle Übergangsfunktion hat die Form
Eine Turingmaschine kann
| akzeptieren | Wenn
|
|---|---|
| verwerfen | Wenn
|
| endlos laufen | Wenn sie niemals abbricht. |
| Fangzustand | Die Turingmaschine kann in einen Fangzustand geraten. In einem Fangzustand arbeitet die Turingmaschine dauernd eine Übergangsfunktion folgender Form ab: Fangzustände können auch formal durch verwerfende Zustände ersetzt werden. |
Mehrbandige Turingmaschinen
Bei mehrbandigen Turingmaschinen hat die Übergangsfunktion die FormEine Konfiguration wird wie folgt dargestellt:

Nichtdeterministische Turingmaschinen
Übergangsfunktion:Die Konfiguration ist ein Baum.
Kosten von Turingmaschinen
Zeitkomplexität:Platzkomplexität:
Ferner gilt:
,da die Turingmaschine auch sofort abbrechen kann. In diesem Fall würden zwar eine Bandzelle besucht aber keine Zeit verbraucht werden. Es würde stehen
Simulation von mehrbandigen Turingmaschinen durch einbandige Turingmaschinen
Jede Mehrbandturingmaschine kann durch eine Einbandturingmaschine simuliert werden und umgekehrt.
,,![]() '': Ist trivial. Jede Einbandturingmaschine kann man auf einer Mehrbandturingmaschine simulieren, indem man nur ein Band der Mehrbandturingmaschine benutzt.
'': Ist trivial. Jede Einbandturingmaschine kann man auf einer Mehrbandturingmaschine simulieren, indem man nur ein Band der Mehrbandturingmaschine benutzt.
,,![]() '': Man kann aus einer Mehrband-DTM folgendermaßen eine Einband-DTM machen:
'': Man kann aus einer Mehrband-DTM folgendermaßen eine Einband-DTM machen:
- Man erweitert die DTM auf auf
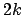 Bänder. Jeweils auf dem
Bänder. Jeweils auf dem 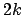 -ten Band setht ein Zeichen, welches die Zeigerposition zeigt, auf dem
-ten Band setht ein Zeichen, welches die Zeigerposition zeigt, auf dem 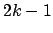 -ten Band ist dsa normale Band zu finden.
-ten Band ist dsa normale Band zu finden.
- Nun erweitert man das Bandalphabet so, daß zu jeder Kombination an Zeichen auf den Bandzellen ein Zeichen in diesem Alphabet vorhanden ist:
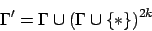
Weiterhin wird auch die Zustandsmenge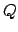 in
in 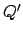 verändert. In den Zuständen
verändert. In den Zuständen 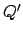 ist für jeden Zustand
ist für jeden Zustand 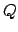 eine Zustandsmenge vorhanden. In dieser werden die Zeichen, die unter den Zeigern der Mehrbandturingmaschine stehen gespeichert und dann hinterher eine Bewegung auf allen virtuellen Bändern ausgeführt5.
eine Zustandsmenge vorhanden. In dieser werden die Zeichen, die unter den Zeigern der Mehrbandturingmaschine stehen gespeichert und dann hinterher eine Bewegung auf allen virtuellen Bändern ausgeführt5.
- Wir verfahren nun bei der Simulation wie folgt:
- Wir suchen alle Zeiger auf dem Band und speichern sie in dem Zustand ab.
- Wir verändern das Band gemäß der original Übergangsfunktion.
- Wir stellen den Zeiger der Einbandturingmaschine wieder vor den ersten im Band kodierten Zeiger.
Die Anzahl der Konfigurationswechsel der simulierenden DTM
wobei
Es gilt auch
Programmierung von DTMs
HintereinanderschaltungMan vereinigt beide Zustandsmengen6. Alle Endzustände der ersten DTM
Schleifen, bedingte Anweisungen usw.
Wir konstruieren eine DTM, die die Bedingung überprüft. Abhängig von der Ausgabe dieser DTM führen wir in die eine oder die andere DTM mit Hilfe des Zustandsmengenwechsels über.
Unterprogramme
Es gibt Zustände, in denen Kontrollinformationen mitgespeichert werden (z.B. Rücksprungadressen). Lokale Variablen von Unterprogrammen können auf einem Extraband gespeichert werden. Die wirft jedoch Probleme bei der Rekursion auf. Besser ist es, sie nacheinander an Stellen des zweiten Bandes zu speichern und sie mit entsprechenden Sonderzeichen von anderen Unterprogrammvariablen zu trennen.
Fußnoten
- ... Turingmaschine4
- Man schreibt leicht ,,Touringmaschine''. Aber Turingmaschinen kommen gar nicht auf Touren, sondern sie sind einfach nur Turingmaschinen ohne o.
- ... ausgeführt5
- Die Zustände haben die Form
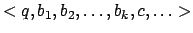 , wobei
, wobei
 . Das ,,
. Das ,,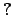 '' steht dafür, daß das Zeichen auf dem betreffenden Band noch nicht bekannt ist
'' steht dafür, daß das Zeichen auf dem betreffenden Band noch nicht bekannt ist
- ... Zustandsmengen6
- Dabei darf natürlich dann kein Zustand mit selben Namen einmal überschrieben werden.