Unterabschnitte
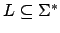 .
. 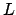 hat die Präfixeigenschaft, wenn für alle Wörter
hat die Präfixeigenschaft, wenn für alle Wörter 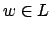 gilt:
gilt:
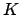 ein DKA
ein DKA
- Definition Präfixeigenschaft
- Deterministische kontextfreie Sprachen mit Präfixeigenschaft werden von DKAs mit Leerer-Keller-Akzeptanz entschieden
Präfixeigenschaft
Weil der Keller bei DKAs leer läuft, ist das Präfix des zu untersuchenden Wortes schon selbst ein Wort der Sprache, benötigen wir die Präfixeigenschaft für alle Wörter der Sprache. Das bedeutet, daß in der Sprache ein Wort niemals echtes Präfix eines anderen Wortes ist.Definition Präfixeigenschaft
Sei
Ist 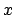 ein echtes Präfix von
ein echtes Präfix von 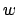 so gilt
so gilt 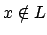
Deterministische kontextfreie Sprachen mit Präfixeigenschaft werden von DKAs mit Leerer-Keller-Akzeptanz entschieden
Sei-
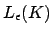 ist deterministisch kontextfrei, d.h.
ist deterministisch kontextfrei, d.h. 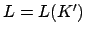 für einen DKA
für einen DKA 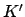 .
.
-
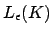 hat Präfixeigenschaft
hat Präfixeigenschaft
- Wenn wir aus einem DKA eine Grammatik machen und dann aus dieser wieder einen NKA, so ist die auch ein DKA.
- Falls die Sprache keine Präfixeigenschaft hat, also
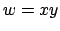 und
und
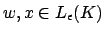 , so verwirft die DKA bei leerer Kellerakzeptanz in der Konfiguration
, so verwirft die DKA bei leerer Kellerakzeptanz in der Konfiguration
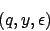
wenn der Keller leer ist. Wenn aber die Sprache Präfixeigenschaft hat, so läuft die DKA mit Leerer-Keller-Akzeptanz bis zum Ende.
Des weiteren gibt es auch zu jeder deterministischen kontextfreien Grammatik mit Präfixeigenschaft einen DKA mit Leerer-Keller Akzeptanz.
Um dies zu beweisen simulieren wir den DKA mit einem DKA mit Leerer-Keller-Akzeptanz. Wir legen zu Beginn das Symbol ![]() auf den Stack. Geraten wir ein einen Endzustand, so entleeren wir den Stack ganz, so daß der DKA akzeptiert. Es ist klar das ein solcher simulierender DKA eine deterministische kontextfreie Grammatik mit Präfixeigenschaft akzeptiert, da der Keller niemals ganz leer wird, sondern das nur am Ende tut.
auf den Stack. Geraten wir ein einen Endzustand, so entleeren wir den Stack ganz, so daß der DKA akzeptiert. Es ist klar das ein solcher simulierender DKA eine deterministische kontextfreie Grammatik mit Präfixeigenschaft akzeptiert, da der Keller niemals ganz leer wird, sondern das nur am Ende tut.