Ψ Die Informatikseite

Unterabschnitte

• Satz von Myhill & Nerode
• Definition: Minimalautomat
• Minimierungsalgorithmus

---

Minimierung von endlichen Automaten

Satz von Myhill & Nerode

Eine Sprache ist genau dann regulär, wenn der Index ihrer Äquivalenzklassen endlich ist⁵³.

Definition: Minimalautomat

Der Automat einer Sprache hat mindestens so viele Zustände, wie die Sprache Äquivalenzklassen hat. Einen Automaten mit minimal vielen Zuständen nennt man Minimalautomat.

Der Minimalautomat eines DFAs unterscheidet sich höchstens in der Benennung der Zustände. Der Minimalautomat eines NFAs kann sich auch in der Art seiner Übergänge unterscheiden.

Minimierungsalgorithmus

1. Wir erstellen eine Tabelle, in der wir jedes Zustandspaar 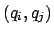eintragen, wobei 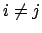gelten muß. (Also nicht einen Zustand mit sich selbst.)
   
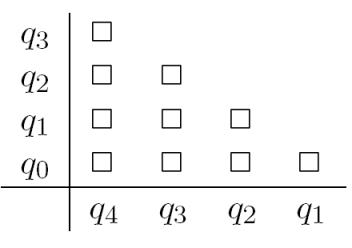
2. Wir markieren in dieser Tabelle alle Zustandspaare, bei denen ein Zustand Endzustand ist.
3. Wir markieren weiterhin alle Zustandspaare, für die gilt
   
   
   
   
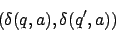
   ist schon markiert. (Das heißt für ein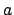 ist schon das Folgezustandspaar markiert) Dabei reicht es, wenn dies für ein 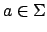gilt.
   Das testen die einzelnen Zustandspaare solange, bis sich in der gesamten Tabelle nichts mehr ändern kann.
4. Wir können die nicht markierten Zustandspaare zusammenfügen.

---

Fußnoten

... ist⁵³

Der Beweis hierfür wird für den Beweis des Minimalisierungsalgorithmusses gebraucht

---