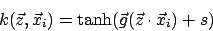Kernel functions
Aber wir können sogenannte Kernel-Functions benutzen. Diese müssen die Mercer-Bedingung erfüllen. Mit der Kernelfunction können wir die Duale Form und die Decision Function dann doch berechnen:Maximiere
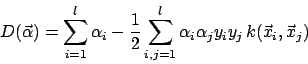
Decision Function ist
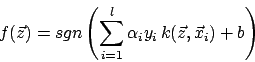
Beispiele für Kernel Functions:
- Polynom Klassifikation
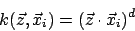
- RBF
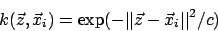
- MLP