Ψ Die Informatikseite

Menü
Informatik » Master » Neuronale Netze » SVMs (Support Vector Machines) » Definition des Risikos zu Support Vector Machines (SVM)
VC-Dimension SVMs (Support Vector Machines) Gute Generalisierung bei Support Vector Machines (SVM)

Definition des Risikos zu Support Vector Machines (SVM)

Wir ziehen aus einer Menge von Mustern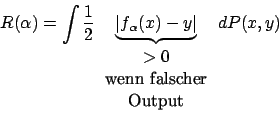 $l$ Muster, die einer Zufallsverteilung $p(x,y)$ gehorchen. Wir können nun ein Risiko formulieren, dass von einer Funktion $f_{\alpha}$ diese Mustermenge nicht spariert werden kann:

\begin{displaymath}R(\alpha)=\int \frac{1}{2}\underbrace {\vert f_{\alpha}(x)-y\... ...}>0\\ \mbox{wenn falscher}\\ \mbox{Output}\end {array}} dP(x,y)\end{displaymath}

Wir können dieses Integral leider nicht berechnen. Aber wir können das impirische Risiko für $l$ Muster berechnen

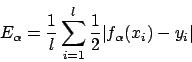
\begin{displaymath}E_{\alpha}=\frac{1}{l}\sum^{l}_{i=1}\frac{1}{2}\vert f_{\alpha}(x_{i})-y_{i}\vert\end{displaymath}

Jedoch repräsentiert $E_{\alpha}$ nicht immer $R(\alpha)$. Es kann sein, dass wir unsere Funktion $f$ so schlecht gewählt haben, dass gerade die gewählten Muster auf sie passen und keinen Fehler haben (das ist zum Beispiel bei einer Tabelle der Fall) und das emprische Risiko $0$ ist, aber das reale Risiko sehr hoch. Deshalb können wir das reale Risiko vom empirischen Risiko nur mit einem Vertrauensterm ableiten:

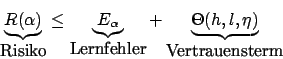
\begin{displaymath}\underbrace{R(\alpha)}_{\mbox{Risiko}}\leq \underbrace{E_{\al... ...nfehler}}+\underbrace{\Theta(h,l,\eta)}_{\mbox{Vertrauensterm}}\end{displaymath}

Der Vertrauensterm ist

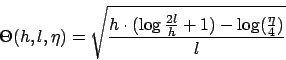
\begin{displaymath}\Theta(h,l,\eta)=\sqrt{\frac{h\cdot(\log\frac{2l}{h}+1)-\log(\frac{\eta}{4})}{l}}\end{displaymath}

  • Die Gleichung für das empirische Risiko gilt mit einer Wahrscheinlichkeit von $1-\eta$.

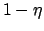    Wenn wir mit einer hohen Wahrscheinlichkeit sagen wollen, dass die Risikogleichung richtig ist, dann erhalten wir einen hohen Wert für den Vertrauesterm z.B.

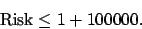
    \begin{displaymath}\mbox{Risk}\leq 1+100000.\end{displaymath}

    Damit können wir allerdings nichts anfangen. Wenn wir auf der anderen Seite mit einer kleinen Wahrscheinlichkeit sagen wollen, dass die Gleichung auch wirklich richtig ist, wird der Vertrauensterm klein. Das nützt aber gar nichts, weil die Gleichung dann nichts mehr aussagt.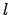
  • $l$ ist die Anzahl der Muster. Um den Vertrauensterm zu verkleinern können wir die Anzahl der Muster groß machen.
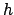  • $h$ ist die VC-Dimension. Wir müssen die VC-Dimension klein machen, um den Vertrauensterm klein zu halten.
VC-Dimension SVMs (Support Vector Machines) Gute Generalisierung bei Support Vector Machines (SVM)