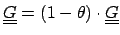Wir haben unter Umständen sehr komplizierte
Controller (Agenten) mit vielen Parametern. Dieser Agent ist in diesem Falle ein neuronales Netz, z.B. zwei-Schicht Perzeptron. Ein neuronales Netz, das
Trainingsnetz,
stellt die Parameter des Controllers ein. Problem ist, dass wir für das Trainingsnetz gar keinen Teacher haben und so gar kein Backpropagation machen können. Wir lernen mit einem Critic. Dieser vergleicht die beiden letzten Rewards und sagt dem Trainingsnetz, dass es die neue Änderung lernen soll, wenn der Reward größer wurde.
Eine Änderung erstellen wir dadurch, indem wir ganz einfach Würfeln (SARO).
- Output des Netzes
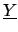 erstellen
erstellen
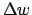 durch die aktuellen Gewichtswerte des Trainingsnetzes berechnen
durch die aktuellen Gewichtswerte des Trainingsnetzes berechnen
- Diese Gewichtswerte auf die Gewichtswerte des Controllers aufaddieren:
- Einen weiteren Output erstellen
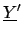
- Critic vergleicht die beiden Outputs und bewertet: Ist die Gewichtsänderung
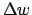 gut, dann
gut, dann 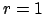 , schlecht, dann
, schlecht, dann 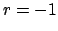
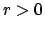 : Es war die richtige Richtung.
: Es war die richtige Richtung. 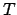 lernt mit modifizierter
lernt mit modifizierter 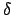 -Regel, indem wir alle Gewichte in die vom
-Regel, indem wir alle Gewichte in die vom 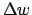 vorgeschlagene Richtung drehen.
vorgeschlagene Richtung drehen.
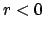 : Es wird verworfen. Wir drehen an allen Gewichten etwas zurück. Das reicht uns jedoch noch nicht, sondern wir addieren auf die Gewichtsmatrix eine zufällige Gewichtsmatrix mit kleinen Werten auf, um durch Würfeln rechtwinklig in dem Raum der Gewichte für den Controller abzubiegen.
: Es wird verworfen. Wir drehen an allen Gewichten etwas zurück. Das reicht uns jedoch noch nicht, sondern wir addieren auf die Gewichtsmatrix eine zufällige Gewichtsmatrix mit kleinen Werten auf, um durch Würfeln rechtwinklig in dem Raum der Gewichte für den Controller abzubiegen.
- Vergessen, d.h. Gewichte Richtung
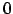 drücken
drücken
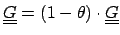
![\includegraphics[scale=0.5]{saro.eps}](img208.png)
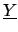 erstellen
erstellen
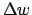 durch die aktuellen Gewichtswerte des Trainingsnetzes berechnen
durch die aktuellen Gewichtswerte des Trainingsnetzes berechnen
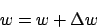
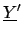
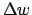 gut, dann
gut, dann 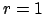 , schlecht, dann
, schlecht, dann 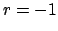
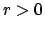 : Es war die richtige Richtung.
: Es war die richtige Richtung. 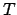 lernt mit modifizierter
lernt mit modifizierter 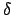 -Regel, indem wir alle Gewichte in die vom
-Regel, indem wir alle Gewichte in die vom 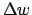 vorgeschlagene Richtung drehen.
vorgeschlagene Richtung drehen.
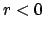 : Es wird verworfen. Wir drehen an allen Gewichten etwas zurück. Das reicht uns jedoch noch nicht, sondern wir addieren auf die Gewichtsmatrix eine zufällige Gewichtsmatrix mit kleinen Werten auf, um durch Würfeln rechtwinklig in dem Raum der Gewichte für den Controller abzubiegen.
: Es wird verworfen. Wir drehen an allen Gewichten etwas zurück. Das reicht uns jedoch noch nicht, sondern wir addieren auf die Gewichtsmatrix eine zufällige Gewichtsmatrix mit kleinen Werten auf, um durch Würfeln rechtwinklig in dem Raum der Gewichte für den Controller abzubiegen.
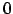 drücken
drücken