Unterabschnitte
![\includegraphics[scale=0.5]{perzeptron.eps}](img16.png) Das Perzeptron
Das Perzeptron 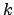 besteht von oben nach unten
besteht von oben nach unten
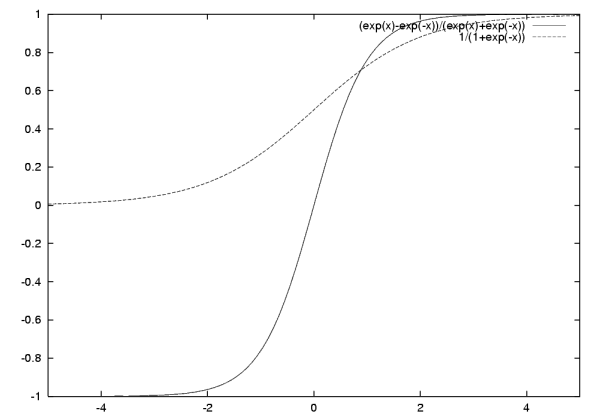
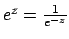

Einzelnes Neuron
Das MLP besteht aus vielen einzelnen Neuronen. MLP steht für Multilayerperzeptron. Häufig wird ein solches neuronales Netz jedoch auch als Perzeptron bezeichnet, so dass Verwechslungsgefahr zu wirklich einzelnen Perzeptrons besteht.Aufbau
![\includegraphics[scale=0.5]{perzeptron.eps}](img16.png)
- aus
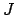 Eingängen. Jeder Eingang hat einen Wert mit
Eingängen. Jeder Eingang hat einen Wert mit
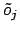 bezeichnet,
bezeichnet,
- einem Eingang
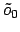 , welcher immer
, welcher immer 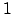 ist. Dies wird für den Schwellwert (BIAS) benötigt.
ist. Dies wird für den Schwellwert (BIAS) benötigt.
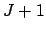 Gewichten. Die Zählung beginnt bei dem Gewicht für den Schwellwert mit
Gewichten. Die Zählung beginnt bei dem Gewicht für den Schwellwert mit 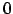 und läuft bis
und läuft bis 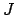 . Die Gewichte werden angegeben mit
. Die Gewichte werden angegeben mit
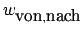 . Siehe dazu auch rechts stehendes kleines Bild. Die Gewichte vom vorhergehenden Neuron oder von der Eingabe werden mit ausgefüllten Kreisen angegeben. Das eine Gewicht für den Schwellwert (BIAS) hat einen unausgefüllten Kreis.
. Siehe dazu auch rechts stehendes kleines Bild. Die Gewichte vom vorhergehenden Neuron oder von der Eingabe werden mit ausgefüllten Kreisen angegeben. Das eine Gewicht für den Schwellwert (BIAS) hat einen unausgefüllten Kreis.
- der Summe
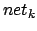 . Summiert werden die Produkte aus den Eingaben und den Gewichten. (incl. BIAS-Gewicht mit 1-Eingabe)
. Summiert werden die Produkte aus den Eingaben und den Gewichten. (incl. BIAS-Gewicht mit 1-Eingabe)
- der Aktivierungsfunktion (auch Transferfunktion, Schwellfunktion, Neuronenfunktion ... genannt)
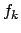 . Die Eingabe dieser Funktion ist die Summe
. Die Eingabe dieser Funktion ist die Summe 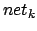 .
.
- der Ausgabe
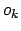 . Sie wird berechnet durch
. Sie wird berechnet durch
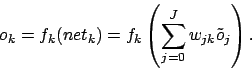
- die Gewichte der nächsten Schicht werden mit
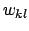 bezeichnet.
bezeichnet.
Aktivierungsfunktionen (Transferfunktionen)
Es gibt verschiedene Aktivierungsfunktionen, die eingesetzt werden können, um die Netzsumme in die Ausgabe zu verrechnen. Die Aktivierungsfunktion sollte- streng monoton steigend
- differenzierbar (einige Funktionen (Sprungfunktion) sind nicht differenzierbar; sie funktionieren so nicht im Backpropagation-Verfahren)
- nach oben und nach unten beschränkt (die lineare Funktion ist nicht beschränkt)
- Werte zwischen
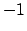 und
und 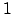 oder
oder 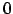 und
und 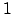 (die lineare Funktion liefert keine Werte dazwischen, sondern auch viel größere bzw. kleinere Werte)
(die lineare Funktion liefert keine Werte dazwischen, sondern auch viel größere bzw. kleinere Werte)
- Wendepunkt bei
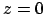
- Lineare Kennlinie (Identität):
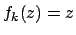
![\includegraphics[scale=0.5]{lineare_kennlinie.eps}](img33.png)
- Sprungfunktion (Stufenfunktion, Heoviside Funktion):

![\includegraphics[scale=0.5]{sprung_funktion.eps}](img35.png)
- Fermifunktion (Logistische Funktion, eine sigmoide Funktion):
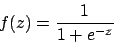
![\includegraphics[scale=0.5]{fermi.eps}](img37.png)
- Tangenshyperbolikus:
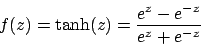
![\includegraphics[scale=0.5]{tanh.eps}](img39.png)

Umrechnung Tangenshyperbolicus in Fermifunktion
Der Tangenshyperbolicus läßt sich in die Fermifunktion umrechnen. Hierbei benutzen wir