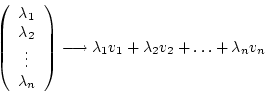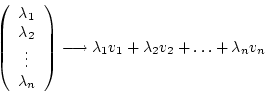Ψ Die Informatikseite

Menü
Informatik » Bachelor » Lineare Algebra » Abbildungen, insbesondere lineare » Isomorphismen
Auswertungsabbildungen Abbildungen, insbesondere lineare Matrizen

Isomorphismen

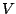
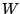
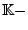
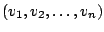
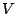
Seien $V$ und $W$ $\mathbb{K}-$Vektorräume. $(v_{1},v_{2},\ldots,v_{n})$ die Basis des Vektorraums $V$. Die Abbildung $f:V\rightarrow W$ ist genau dann ein Isomorphismus4.3, wenn

\begin{displaymath}(f(v_{1}),f(v_{2}),\ldots,f(v_{n}))\end{displaymath}

eine Basis von $W$ ist. Der Satz gilt auch umgekehrt.
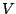
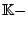
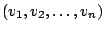
Sei $V$ ein $\mathbb{K}-$Vektorraum und $(v_{1},v_{2},\ldots,v_{n})$ seine Basis. Wir nennen den Isomorphimus

\begin{displaymath}\mathbb{K}^{n}\longrightarrow V\end{displaymath}


\begin{displaymath}\left(\begin {array}{c}\lambda_{1}\\ \lambda_{2}\\ \vdots\\ \... ...arrow \lambda_{1}v_{1}+\lambda_{2}v_{2}+\ldots+\lambda_{n}v_{n}\end{displaymath}

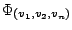
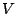
kanonischen Basisisomorphimus. Bei Bedarf bezeichnet man ihn mit $\Phi_{(v_{1},v_{2},v_{n})}$. Wir sehen hier, dass wir die Definition des kanonischen Basisisomorphimusses ausnutzen können, um aus einer Basis mit Einheitsvektoren (die kanonische Basis) und den Basisvektoren des Vektorraums $V$ eine Matrix zu machen, die zwischen den beiden Vektorräumen transformiert. 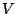Wir tun dies einfach, indem wir die Vektoren der Basis von $V$ hineinander in die Matrix schreiben.


Auswertungsabbildungen Abbildungen, insbesondere lineare Matrizen