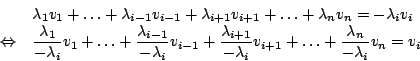Seien
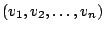
eine Familie von Vektoren in einem
Vektorraum. Jeder Vektor
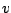
der Form
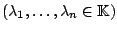
heißt
Linearkombination von
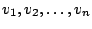
.
Es folgen nun einige Beweise, zwischen den Begriffen ,,linear (un)abhängig'' und ,,Linearkombination''. Die Folgerungen dieser Beweise werden wahrscheinlich den meisten Lesern schon in Fleisch und Blut übergegangen sein. Sie wissen einfach, dass es so ist. Eigentlich müssen wir das aber erst einmal beweisen:
Satz: Wenn die Vektoren der Familie
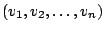 linear unabhängig zueinander sind, dann kann jeder Vektor
linear unabhängig zueinander sind, dann kann jeder Vektor
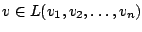 durch sie nur auf eine bestimmte Weise kombiniert werden
Aus
durch sie nur auf eine bestimmte Weise kombiniert werden
Aus
folgt also
Beweis:
Wegen der linearen Unabhängigkeit gilt nun:
Somit kann der Vektor nur auf eine Weise kombiniert werden.
Umgekehrt kann man beweisen:
Satz: Wenn jeder Vektor 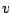 nur auf eine Weise aus der Familie
nur auf eine Weise aus der Familie
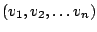 linear kombiniert werden kann, dann sind die Vektoren der Familie linear unabhängig zueinander.
linear kombiniert werden kann, dann sind die Vektoren der Familie linear unabhängig zueinander.
Nur auf eine Weise kombinierbar bedeutet, dass wenn
gilt,
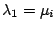
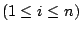
gilt und somit
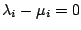
.
Da
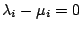
für
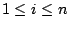
sind die Vektoren der Familie linear unabhängig.
Satz: Wenn die Vektoren einer Familie
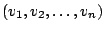
jedoch linear abhängig sind, dann gibt es mehr als eine Möglichkeit einen Vektor
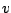
zu kombinieren. Lineare Abhängigkeit bedeutet ja, dass für mindestens ein
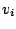
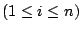
gilt:
Beweis:
Wenn wir nun den Vektor
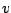
haben, können wir ihn auf folgende Weise kombinieren:
Wir erhalten hieraus
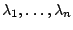
. Nun können wir jedoch die oben genannte Linearkombination für
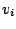
einsetzen und erhalten
Also ist
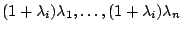
eine neue Möglichkeit
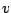
zu kombinieren und somit haben wir schon
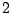
Möglichkeiten.
Wir können auch die folgenden beiden Tatsachen beweisen:
Satz: Wenn sich kein Vektor 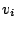 der Familie
der Familie
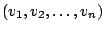 linear aus der Familie
linear aus der Familie
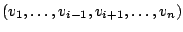 kombinieren läßt, so sind die Vektoren der Familie
kombinieren läßt, so sind die Vektoren der Familie
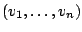 linear unabhängig zueinander.
linear unabhängig zueinander.
Beweis:
Angenommen, sei seien linear abhängig. Das bedeuet, dass für
für mindestens ein
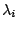
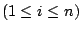
gilt
Das bedeutet
Dann läßt sich
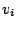
aus
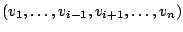
linear kombinieren. Widerspruch zur Voraussetzung. Also müssen die Vektoren linear unabhängig sein.
Ebenso gilt umgekehrt:
Satz: Wenn die Vektoren der Familie
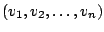
linear unabhängig zueinander sind, so läßt sich keiner der Vektoren aus dem anderen linear kombinieren.
Beweis:
Angenommen, das geht doch; es läßt sich ein Vektor
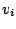
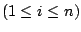
linear kombinieren. Dann gilt:
Daraus folgt durch Subtrahieren von
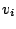
:
Wir sehen, dass
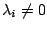
ist, da
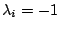
. Also wären die Vektoren der Familie linear abhängig. Widerspruch. Es ist also nicht möglich, dass einer der Vektoren Linearkombination der anderen ist, weil sonst die lineare Unabhängigkeit verletzt ist.
![]() linear unabhängig zueinander sind, dann kann jeder Vektor
linear unabhängig zueinander sind, dann kann jeder Vektor
![]() durch sie nur auf eine bestimmte Weise kombiniert werden
Aus
durch sie nur auf eine bestimmte Weise kombiniert werden
Aus
![]() nur auf eine Weise aus der Familie
nur auf eine Weise aus der Familie
![]() linear kombiniert werden kann, dann sind die Vektoren der Familie linear unabhängig zueinander.
linear kombiniert werden kann, dann sind die Vektoren der Familie linear unabhängig zueinander.
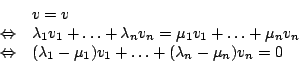

![]() der Familie
der Familie
![]() linear aus der Familie
linear aus der Familie
![]() kombinieren läßt, so sind die Vektoren der Familie
kombinieren läßt, so sind die Vektoren der Familie
![]() linear unabhängig zueinander.
linear unabhängig zueinander.