Unterabschnitte
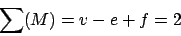
mit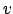
als Anzahl der Knoten, 
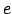als Anzahl der Kanten und 
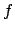als Anzahl der Facetten ist für zu einer Kugel (ohne Henkel) homöomorphen Polyedern konstant, unabhängig davon, wie wir die Unterteilung der einzelnen Polygone wählen. Dies ist jedoch nur eine notwendige Bedingung. Sie ist nicht hinreichend und kann dann zur Verifikation von Polyedern verwendet werden, ob diese zu einer Kugel homöomorph sind.
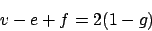
Dabei ist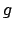
die Anzahl der Henkel und heißt ,,Geschlecht'' der Kugel.
- Orientierbarkeit von Facetten
- Gleichorientiert
- Orientierbares Polygonnetz
- Zerlegung in Tetraeder bzw. Dreiecke
- Euler Formel
- Kugeln mit Henkeln
Eigenschaften von Polyedern
Orientierbarkeit von Facetten
Polygonnetze lassen sich orientieren. Entweder die Punkte werden mit dem Uhrzeigersinn nacheinander benannt oder gegen den Uhrzeigersinn.Gleichorientiert
Zwei Facetten eines Polyeders, welche beide die gleiche Durchlaufrichtung also Orientierung der Punkte haben, heißen gleichorientiert. Dabei wird dann die gemeinsame Kante entgegengesetzt durchlaufen.Orientierbares Polygonnetz
Ein Polygonnetz heißt orientierbar, wenn die Facetten des Netzes so orientiert werden können, dass zwei benachbarte Facetten gleichorientiert sind. Nicht alle Flächen sind orientierbar. Ausnahmen bilden z.B. das Berühmte Möbius-Band oder die Kleinsche Flasche.Zerlegung in Tetraeder bzw. Dreiecke
- Polyeder sind nicht unbedingt in Tetraeder zerlegbar.
- Allerdings lassen sich alle Polygone in Dreiecke zerlegen.
Euler Formel
Die Summe
mit
als Anzahl der Knoten, als Anzahl der Kanten und als Anzahl der Facetten ist für zu einer Kugel (ohne Henkel) homöomorphen Polyedern konstant, unabhängig davon, wie wir die Unterteilung der einzelnen Polygone wählen. Dies ist jedoch nur eine notwendige Bedingung. Sie ist nicht hinreichend und kann dann zur Verifikation von Polyedern verwendet werden, ob diese zu einer Kugel homöomorph sind.
Kugeln mit Henkeln
Ist ein Polyeder homöomorph zu einer Kugel mit einem oder mehreren Henkeln, so gilt
Dabei ist
die Anzahl der Henkel und heißt ,,Geschlecht'' der Kugel.