Unterabschnitte
Die Laufzeit hierfür ist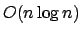 , für das Sortieren der Linien, jeweils
, für das Sortieren der Linien, jeweils 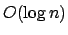 für das Einfügen und Löschen in den AVL-Blattbäumen an jedem Haltepunkt der Scanline. Macht zusammen die Laufzeit
für das Einfügen und Löschen in den AVL-Blattbäumen an jedem Haltepunkt der Scanline. Macht zusammen die Laufzeit 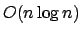
Die Laufzeit hierfür ist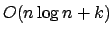 , wobei k die Anzahl der Schnitte ist.
, wobei k die Anzahl der Schnitte ist.
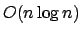 , da die Sortierung der Haltepunkte die Laufzeit des Sortierverfahrens beansprucht (
, da die Sortierung der Haltepunkte die Laufzeit des Sortierverfahrens beansprucht (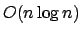 ) und an jedem Haltepunkt eine kostante Anzahl an Operationen, nämlich eine Lösch oder Einfügeoperation und ein oder zwei Schnitttests stattfinden.
) und an jedem Haltepunkt eine kostante Anzahl an Operationen, nämlich eine Lösch oder Einfügeoperation und ein oder zwei Schnitttests stattfinden.
Das hier vorgestellte Verfahren untersucht übrigens nur einen Schnittpunkt. Es kann sein, daß eine Gerade mehrmals andere Geraden schneidet. Um dies zu überprüfen benötigen wir eine Umsortierung des AVL-Blattbaumes.
- Sichtbarkeitsproblem für horizontale Objekte
- Schnittproblem für horizontale und vertikale Objekte
- Geometrisches Divide&Conquer für horizontal und vertikal liegende Objekte
- Schnittproblem für (fast) beliebig liegende Objekte
- Voronoidiagramme
Scanlines
Sichtbarkeitsproblem für horizontale Objekte
Aktive Linien verwalten wir in einem AVL-Blatt-Baum. Im AVL-Blatt-Suchbaum steht immer die y-Koordinate der Linien. Wir legen für jeden Anfang und jedes Ende einer Linie einen Scanlinestopp an. Kommen wir an den Anfang einer Linie, so aktivieren wir diese, indem wir sie in den AVL-Blatt-Baum einfügen. Wir können die doppelte Verknüpfung der Blätter nutzen, um festzustellen, ob wir direkte sichbare Nachbarn haben. Wenn wir Nachbarn finden, dann geben wir das Nachbarschaftspaar aus. Ähnlich verfahren wir mit dem Ende einer Linie. Wir entfernen sie aus dem AVL-Blatt-Baum und überprüfen danach, ob neue Nachbarschaften entstanden sind und geben diese ggf. aus.Die Laufzeit hierfür ist
Schnittproblem für horizontale und vertikale Objekte
Wir verfahren ähnlich wie oben. Wir fügen Scanlinestopps für jede vertikale Linie ein. Bei jeder vertikalen Linie testen wir, welche Linie im AVL-Blatt-Baum vorhanden sind, die die Linie schneiden. Hierfür kann man wieder die Doppeltverkettung der Blätter gut nutzen.Die Laufzeit hierfür ist
Geometrisches Divide&Conquer für horizontal und vertikal liegende Objekte
Wir unterteilen den Raum, in welchem die Graden enthalten sind, in zwei ungefähr gleich große Räume und führen auf diesen wieder ein Devide und Conquer durch. In unserem Beispiel aus der Vorlesung haben wir den Divide-Schritt nur einmal durchgeführt und dann sofort die Teile ,,geconquert''. Bei der Betrachtung der Teile können folgende Fälle auftreten:- Die vertikale Gerade schneidet die horizontale Gerade nicht.
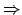 Es gibt keinen Schnittpunkt
Es gibt keinen Schnittpunkt
- Die vertikale Gerade schneidet die horizontale Gerade.
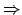 Schnittpunkt ausgeben.
Schnittpunkt ausgeben.
- Die vertikale Gerade schneidet die horizontale Gerade, wobei ein Endpunkt der horizontalen Geraden in dem anderen Teil des vorher in zwei Teile zerteilten Raumes ist.
 Schnittpunkt ausgeben.
Schnittpunkt ausgeben.
- Die vertikale Gerade schneidet die horizontale Gerade, wobei der eine Endpunkt noch nicht einmal in dem anderen Teil des Raumes ist, mit welchem der Raum vor dem Cutschritt noch zusammenhing.
 Auch Schnittpunkt ausgeben.
Auch Schnittpunkt ausgeben.
Schnittproblem für (fast) beliebig liegende Objekte
Wir setzen bei diesem Algorithmus voraus, daß- Die Anfangs und Endpunkte der Geraden von Beginn des Algorithmusses an feststehen.
- Keine Gerade parallel zur y-Achse also genau senkrecht verläuft.
- Sich nicht mehr als zwei Geraden in ein und demselben Punkt schneiden.
Das hier vorgestellte Verfahren untersucht übrigens nur einen Schnittpunkt. Es kann sein, daß eine Gerade mehrmals andere Geraden schneidet. Um dies zu überprüfen benötigen wir eine Umsortierung des AVL-Blattbaumes.
Voronoidiagramme
- Das Voronoidiagramm unterstützt die Suche nach dem Nachbarknoten mit der geringsten Entfernung.
- Die Kanten in diesem Diagramm liegen immer so, daß für benachbarte Knoten die Kante genau in der Mitte liegt. Für zwei benachbarte Knoten sind die Voronoi-Regionen Nachbarn.
- Außen liegende Knoten, für die es keine Nachbarn mehr gibt, heißen unbeschränkte Voronoiregionen. Die Punkte heißen zusammen ,,Konvexe Hülle''.
- Schnittpunkt die die Voronoikanten miteinander bilden, heißen Voronoiknoten.
- Mittes Divide&Conquer kann ein Voronoidiagramm erstellt werden.