Unterabschnitte
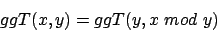
Hierbei werden alle Faktoren, die nicht Primfaktoren beider Zahlen sind, herausgezogen, bis letztendlich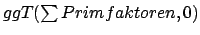 übrigbleibt.
übrigbleibt.
Der Worst-Case-Fall des Euklidalgorithmus sind die Fibonaccizahlen. Die Fibonaccizahlen haben die Eigenschaft, daß wenn man den Rest von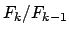 bestimmt,
bestimmt, 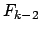 herauskommt, da
herauskommt, da
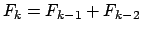 . Es müssen somit genau
. Es müssen somit genau 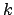 Schritte durchgeführt werden, um darauf zu kommen, daß der ggT zweier Fibonaccizahlen, die im Wort-Case aufeinander folgen,
Schritte durchgeführt werden, um darauf zu kommen, daß der ggT zweier Fibonaccizahlen, die im Wort-Case aufeinander folgen, 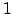 ist.
ist.
Für Fibonaccizahlen gilt
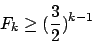
Wir sehen, daß je größer die Zahlen werden, die Häufigkeit der Fibonaccizahlen logarithmisch abnimmt, da die Größe der Fibonaccizahlen exponentiell steigt. Somit gilt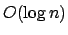 .
.
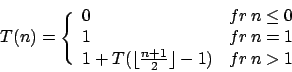
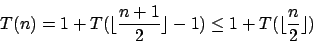
1.Fall: ist eine Zweierpotenz, etwa
ist eine Zweierpotenz, etwa 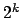
2.Fall: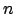 beliebig: Sei
beliebig: Sei
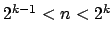
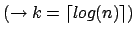
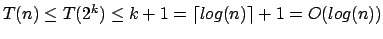
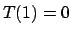
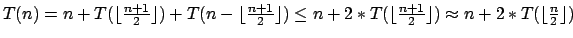
1. Fall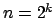 :
:
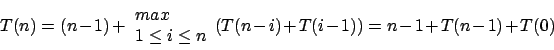
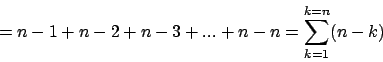
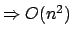
 :
:
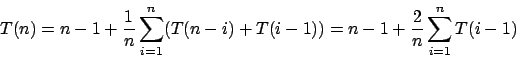
Durch Induktion kann man zeigen (ohne Beweis):
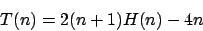
Wobei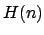 die harmonsische Reihe ist, für die gilt:
die harmonsische Reihe ist, für die gilt:
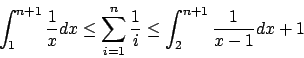
Hiermit läßt sich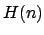 nach
nach 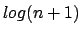 bzw.
bzw. 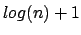 abschätzen. Somit ist die Laufzeit im Average Case:
abschätzen. Somit ist die Laufzeit im Average Case:
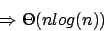
Rekurrenzen
Euklid (Bestimmung des ggTs)
Der Euklidische Algortihmus berechnet den ggT mittels rekursiven Aufrufen1 folgendermaßen:Hierbei werden alle Faktoren, die nicht Primfaktoren beider Zahlen sind, herausgezogen, bis letztendlich
Der Worst-Case-Fall des Euklidalgorithmus sind die Fibonaccizahlen. Die Fibonaccizahlen haben die Eigenschaft, daß wenn man den Rest von
Für Fibonaccizahlen gilt
Wir sehen, daß je größer die Zahlen werden, die Häufigkeit der Fibonaccizahlen logarithmisch abnimmt, da die Größe der Fibonaccizahlen exponentiell steigt. Somit gilt
Binäre Suche
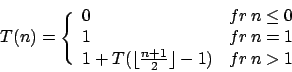
1.Fall:
|
|
|
|
|
|
|
|
|
|
|
2.Fall:
Mergesort
1. Fall
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Quicksort
Worst-Case
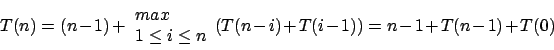
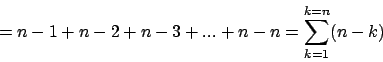
Average Case
Für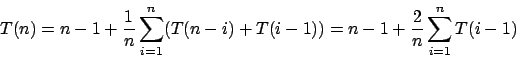
Durch Induktion kann man zeigen (ohne Beweis):
Wobei
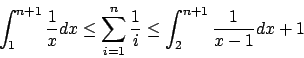
Hiermit läßt sich
Fußnoten
- ... Aufrufen1
- Es gibt auch ein iteratives Verfahren des Euklidischen Algorithmusses.